Теоретическая механика

Отображение 481–512 из 1345

• 

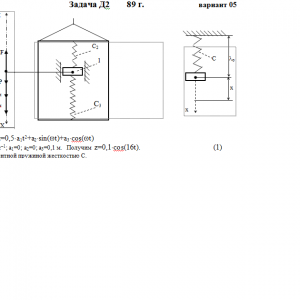
  Тарг 1989 год задача Д2 вариант 05

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=2 кг, с2=400 Н/м, с3=400 Н/м, a1=0 м/с², a2=0 м, a3=0,1 м, ω=16 с^-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

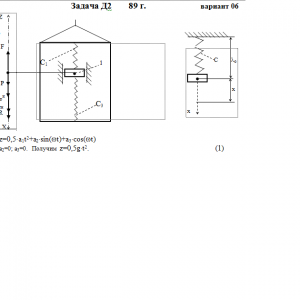
  Тарг 1989 год задача Д2 вариант 06

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,4 кг, с1=60 Н/м, с3=180 Н/м, a1=g м/с², a2=0 м, a3=0 м, μ= 4 Н*с/м, λ0=0 м, V0=2 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

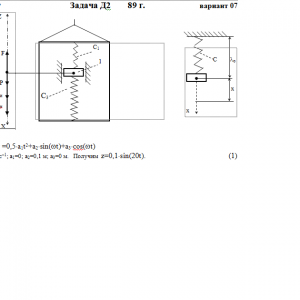
  Тарг 1989 год задача Д2 вариант 07

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,5 кг, с1=120 Н/м, с3=180 Н/м, a1=0 м/с², a2=0,1 м, a3=0 м, ω=20 с^-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

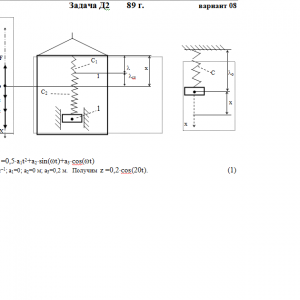
  Тарг 1989 год задача Д2 вариант 08

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,4 кг, с1=50 Н/м, с2=200 Н/м, a1=0 м/с², a2=0 м, a3=0,2 м, ω=20 с^-1, μ= 0 Н*с/м, λ0=0,15 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 09

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=1 кг, с1=200 Н/м, с3=300 Н/м, a1=1,5g м/с², a2=0 м, a3=0 м, μ= 20 Н*с/м, λ0=0 м, V0=3 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 11

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,8 кг, с2=240 Н/м, с3=120 Н/м, a1=-1,5g м/с², a2=0 м, a3=0 м, μ= 48 Н*с/м, λ0=0,1 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 15

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=2 кг, с2=400 Н/м, с3=400 Н/м, a1=-1,5g м/с², a2=0 м, a3=0 м, μ= 48 Н*с/м, λ0=0,1 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

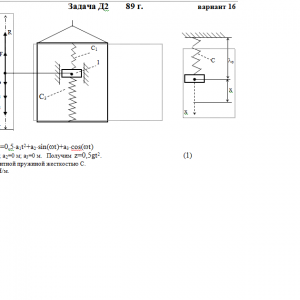
  Тарг 1989 год задача Д2 вариант 16

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,4 кг, с1=60 Н/м, с3=120 Н/м, a1=g м/с², a2=0 м, a3=0 м, μ= 4 Н*с/м, λ0=0 м, V0=2 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 17

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,5 кг, с1=120 Н/м, с3=180 Н/м, a1=0 м/с², a2=0,1 м, a3=0 м, ω= 20 с ^-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

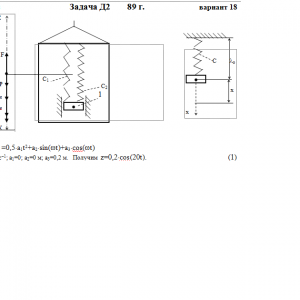
  Тарг 1989 год задача Д2 вариант 18

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,4 кг, с1=50 Н/м, с2=200 Н/м, a1=0 м/с², a2=0 м, a3=0,2 м, ω= 20 с ^-1, μ= 0 Н*с/м, λ0=0,15 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 19

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=1 кг, с1=200 Н/м, с3=300 Н/м, a1=1,5g м/с², a2=0 м, a3=0 м, μ= 20 Н*с/м, λ0=0 м, V0=3 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 21

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,8 кг, с2=240 Н/м, с3=120 Н/м, a1=-1,5g м/с², a2=0 м, a3=0 м, ω= 0 с^-1, μ= 8 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

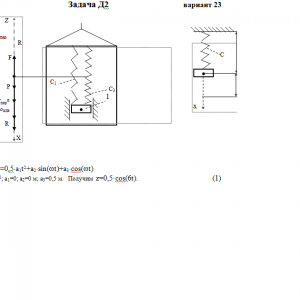
  Тарг 1989 год задача Д2 вариант 23

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=1 кг, с1=240 Н/м, с3=160 Н/м, a1=0 м/с², a2=0 м, a3=0,5 м, ω= 6 с^-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 24

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,5 кг, с1=80 Н/м, с2=120 Н/м, a1= -g м/с², a2=0 м, a3=0 м, ω= 0 с^-1, μ= 6 Н*с/м, λ0=0,15 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

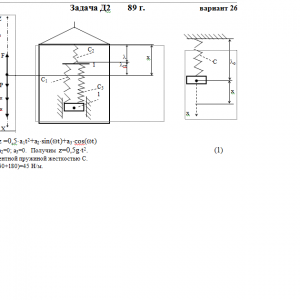
  Тарг 1989 год задача Д2 вариант 26

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,4 кг, с1=60 Н/м, с3=180 Н/м, a1= g м/с², a2=0 м, a3=0 м, μ= 4 Н*с/м, λ0=0 м, V0=2 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 27

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,5 кг, с1=120 Н/м, с3=180 Н/м, a1= 0 м/с², a2=0,1 м, a3=0 м, ω=20 с^-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

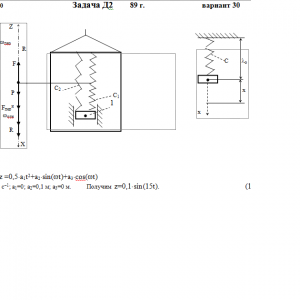
  Тарг 1989 год задача Д2 вариант 30

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=1 кг, с1=300 Н/м, с2=150 Н/м, a1= 0 м/с², a2=0,1 м, a3=0 м, ω=15 с^-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 32

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,5 кг, с2=100 Н/м, с3=150 Н/м, a1= 0 м/с², a2=0,8 м, a3=0 м, ω=5 с^-1, λ0=0 м, V0=4 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 33

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=1 кг, с1=240 Н/м, с3=160 Н/м, a1= 0 м/с², a2=0 м, a3=0,5 м, ω=6 с^-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

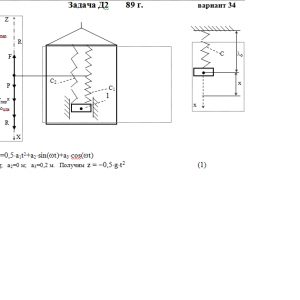
  Тарг 1989 год задача Д2 вариант 34

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,5 кг, с1=80 Н/м, с2=120 Н/м, a1= -g м/с², a2=0 м, a3=0 м, ω=0 с^-1, μ= 6 Н*с/м, λ0=0,15 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

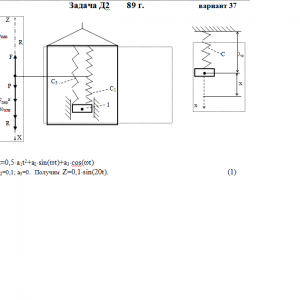
  Тарг 1989 год задача Д2 вариант 37

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,5 кг, с1=120 Н/м, с3=180 Н/м, a1= 0 м/с², a2=0,1 м, a3=0 м, ω=20 с^-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 41

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,8 кг, с1=240 Н/м, с3=120 Н/м, a1= -1,5g м/с², a2=0 м, a3=0 м, ω=0 с^-1, μ= 8 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

  Тарг 1989 год задача Д2 вариант 43

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=1 кг, с1=240 Н/м, с3=160 Н/м, a1= 0 м/с², a2=0 м, a3=0,5 м, ω=6 с^-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

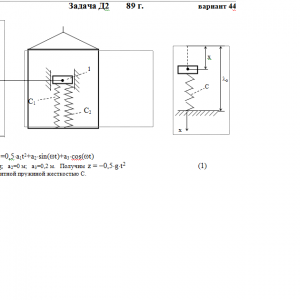
  Тарг 1989 год задача Д2 вариант 44

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,5 кг, с1=80 Н/м, с2=120 Н/м, a1= -g м/с², a2=0 м, a3=0 м, ω=0 с^-1, μ= 6 Н*с/м, λ0=0,15 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

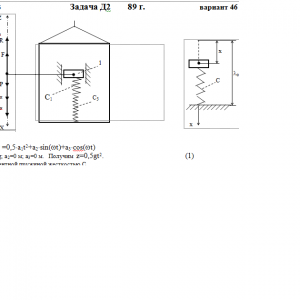
  Тарг 1989 год задача Д2 вариант 46

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,4 кг, с1=60 Н/м, с3=120 Н/м, a1= g м/с², a2=0 м, a3=0 м, μ= 4 Н*с/м, λ0=0 м, V0=2 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

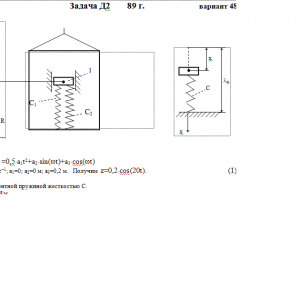
  Тарг 1989 год задача Д2 вариант 48

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,4 кг, с1=50 Н/м, с2=200 Н/м, a1= 0 м/с², a2=0 м, a3=0,2 м, ω=20 с^-1, μ= 0 Н*с/м, λ0=0,15 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

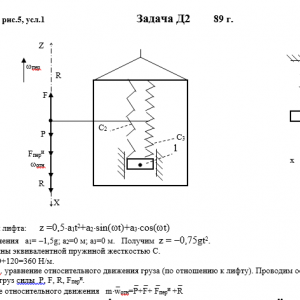
  Тарг 1989 год задача Д2 вариант 51

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,8 кг, с2=240 Н/м, с3=120 Н/м, a1= -1.5 м/с², a2=0 м, a3=0 м, ω=0 с^-1, μ= 8 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

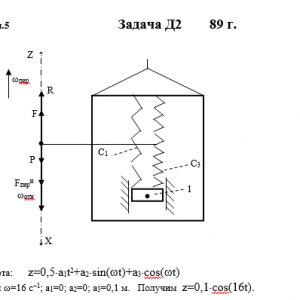
  Тарг 1989 год задача Д2 вариант 55

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=2 кг, с2=400 Н/м, с3=400 Н/м, a1= 0 м/с², a2=0 м, a3=0.1 м, ω=16 с^-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

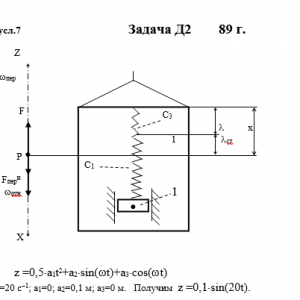
  Тарг 1989 год задача Д2 вариант 57

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,5 кг, с1=120 Н/м, с3=180 Н/м, a1= 0 м/с², a2=0,1 м, a3=0 м, ω=20 с^-1, μ= 0 Н*с/м, λ0= 0,15 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

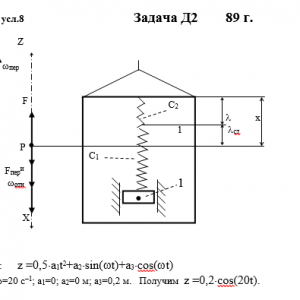
  Тарг 1989 год задача Д2 вариант 58

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,4 кг, с1=50 Н/м, с2=200 Н/м, a1= 0 м/с², a2=0 м, a3=0,2 м, ω=0 с^-1, μ= 0,15 Н*с/м, λ0= 0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

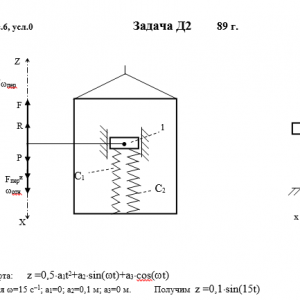
  Тарг 1989 год задача Д2 вариант 60

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=1 кг, с1=300 Н/м, с2=150 Н/м, a1= 0 м/с², a2=0,1 м, a3=0 м, ω=15 с^-1, μ= 0 Н*с/м, λ0= 0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину
• 

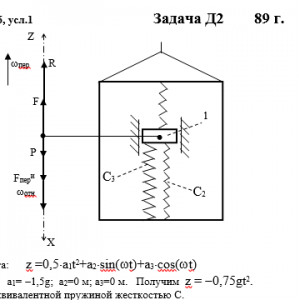
  Тарг 1989 год задача Д2 вариант 61

  Описание

  Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a₁t²+a₂*sin(ωt)+a₃*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
  Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с². Массой пружин и соединительной планки 2 пренебречь.
  В таблице обозначено: с₁, с₂, с₃ — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v₀— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с₁, с₂, с₃ означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
  Условие μ = 0 означает, что сила сопротивления R отсутствует.

  Дано: m=0,8 кг, с2=240 Н/м, с3=120 Н/м, a1= -1,5g м/с², a2=0,1 м, a3=0 м, ω= 48 с^-1, μ= 0,1 Н*с/м, λ0= 0 м, V0=0 м/с
  Найти: x(t)

  1.00 $ В корзину