Математика КрНУ, семестр 3
Методичка в формате pdf — ЗДЕСЬ
Вы можете выбрать один из вариантов заказать решение через форму. В случае если ваше задание отсутствует, перейдите в раздел Заказать новую работу и заполните необходимые поля.
Вы также можете связаться одним из указанных способов:
Возможно решение задач онлайн (необходима предварительная связь).
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
Задание 4. Решить систему дифференциальных уравнений двумя способами: а) методом исключения; б) с помощью характеристического уравнения.
Задание 5. Доказать сходимость ряда и найти его сумму.
Задание 6. Исследовать на сходимость указанные ряды.
Задание 7. Найти область сходимости ряда.
Задание 8. Разложить в ряд Маклорена и Тейлора функцию f(x). Указать область сходимости полученного ряда к этой функции.
Задание 9. Используя разложение подынтегральной функции в степенной ряд, вычислить указанный определённый интеграл с точностью до 0,001.
Задание 10. Найти разложение в степенной ряд по степеням х решения дифференциального уравнения.
Задание 11. Разложить в ряд Фурье периодическую (с периодом ω=2π) функцию f(x), заданную на отрезке.
Задание 12. Разложить в ряд Фурье f(x), заданную в интервале (0; π), продолжив её чётным и нечётным образом. Построить графики для каждого продолжения.
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
Представлено 30 товаров
-

Математика КрНУ, семестр 3, вариант 1, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 10, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 11, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 12, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 13, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 14, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
Методичка с заданием доступна по ссылке:
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 15, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 16, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 17, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
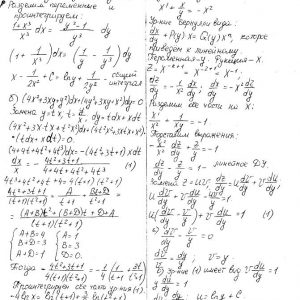
Математика КрНУ, семестр 3, вариант 18, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 19, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 2, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
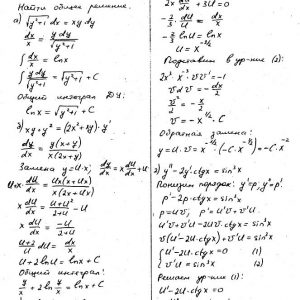
Математика КрНУ, семестр 3, вариант 20, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 21, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
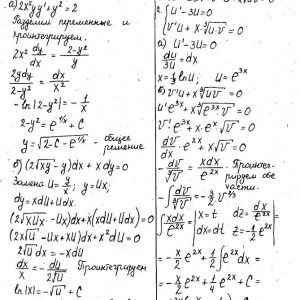
Математика КрНУ, семестр 3, вариант 22, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
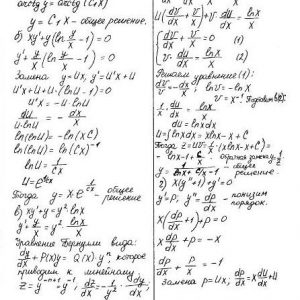
Математика КрНУ, семестр 3, вариант 23, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
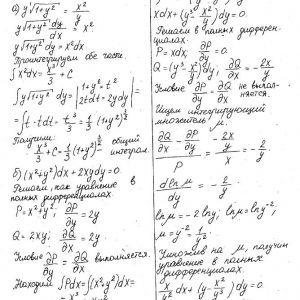
Математика КрНУ, семестр 3, вариант 24, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 25, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
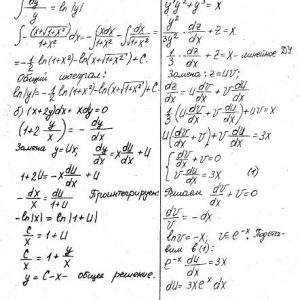
Математика КрНУ, семестр 3, вариант 26, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 27, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 28, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 29, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 3, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 30, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
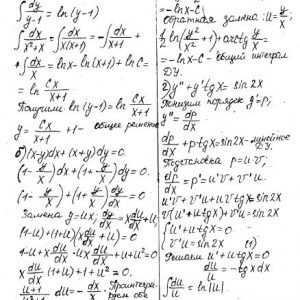
Математика КрНУ, семестр 3, вариант 4, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 5, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
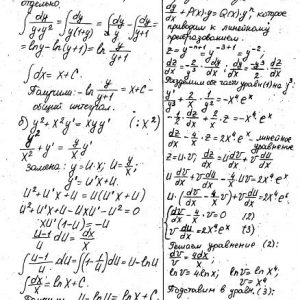
Математика КрНУ, семестр 3, вариант 6, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
Математика КрНУ, семестр 3, вариант 7, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
Математика КрНУ, семестр 3, вариант 8, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 9, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину