Теоретическая механика
Отображение 929–960 из 1345
-

Тарг 1989 год задача Д8 вариант 83
Описание
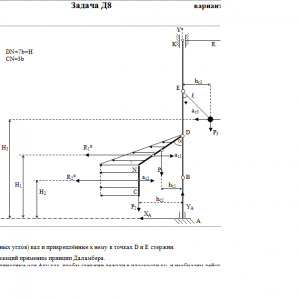
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, γ=60° φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RD -
Тарг 1989 год задача Д8 вариант 84
Описание
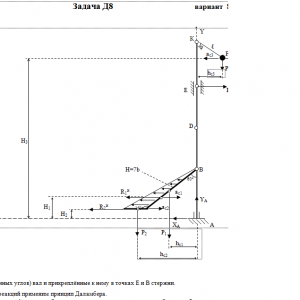
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, γ=150° φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -
Тарг 1989 год задача Д8 вариант 85
Описание
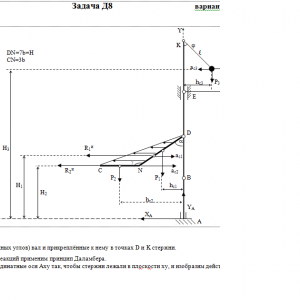
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=45°, γ=135° φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -
Тарг 1989 год задача Д8 вариант 86
Описание
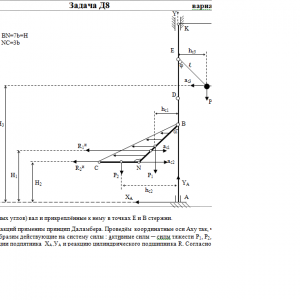
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, γ=150° φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -
Тарг 1989 год задача Д8 вариант 87
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, γ=120° φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -
Тарг 1989 год задача Д8 вариант 88
Описание
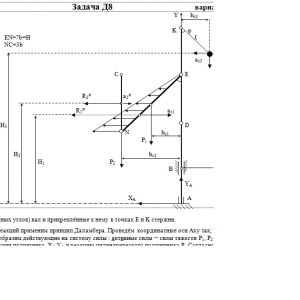
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, γ=60° φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -
Тарг 1989 год задача Д8 вариант 89
Описание
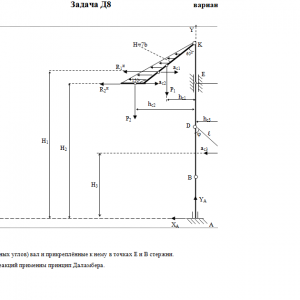
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, γ=150° φ=45°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -
Тарг 1989 год задача Д8 вариант 90
Описание
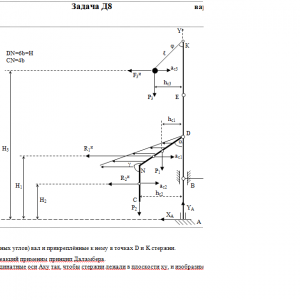
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=45°, γ=225° φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -

Тарг 1989 год задача Д8 вариант 91
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=240° φ=45°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RК -

Тарг 1989 год задача Д8 вариант 93
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=240° φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RD -

Тарг 1989 год задача Д8 вариант 94
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, γ=210° φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -

Тарг 1989 год задача Д8 вариант 95
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=45°, γ=135° φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RЕ -

Тарг 1989 год задача Д8 вариант 96
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, γ=150° φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RЕ -

Тарг 1989 год задача Д8 вариант 97
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, γ=120° φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RК -

Тарг 1989 год задача Д8 вариант 98
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, γ=60° φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -
Тарг 1989 год задача Д8 вариант 99
Описание
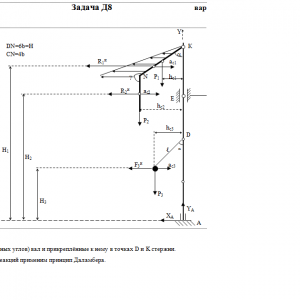
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, γ=210° φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -
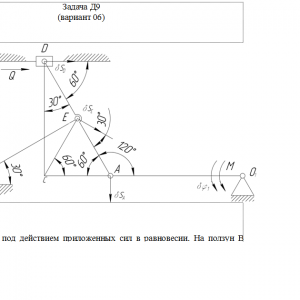
Тарг 1989 год задача Д9 вариант 06
Описание
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами α, β, γ, φ, θ (рис. Д9.0 — Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: l1=0,4 м, l4=0,6 м (размеры l2 и l3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины F, численно F = cλ, где с — коэффициент жесткости пружины, λ—ее деформация. Кроме того, на рис. 0 и 1 на ползун D действует сила Q, а на кривошип О1А — пара сил с моментом М; на рис. 2-9 на кривошипы О1А и О2D действуют пары сил с моментами M1 и М2.
Определить, чему равна при равновесии деформация λ пружины, и указать, растянута пружина или сжата. Значении всех заданных величин приведены в табл. Д9а для рис. 0—4 и в табл. Д9б для рис. 5—9, где Q выражено в ньютонах, а М, M1, М2 — в ньютоно-метрах.
Построение чертежа начинать со стержня, направление которого определяется углом α; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10, б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10. а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10,б, где одновременно иначе изображены направляющие).Дано: механизм находится под действием приложенных сил в равновесии. На ползун В действует сила упругости пружины. Кроме того. На ползун D действует сила Q, а на звено 1 — пара сил с моментом М.
М=220 Н•м, Q=280 Н, с=110 Н/смНайти: чему равна при равновесии деформация пружины и указать, растянута пружина или сжата.
1.00 $ В корзину -
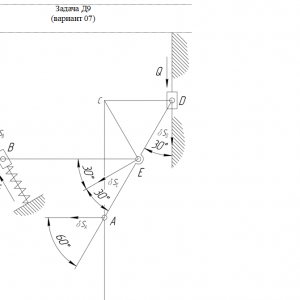
Тарг 1989 год задача Д9 вариант 07
Описание
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами α, β, γ, φ, θ (рис. Д9.0 — Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: l1=0,4 м, l4=0,6 м (размеры l2 и l3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины F, численно F = cλ, где с — коэффициент жесткости пружины, λ—ее деформация. Кроме того, на рис. 0 и 1 на ползун D действует сила Q, а на кривошип О1А — пара сил с моментом М; на рис. 2-9 на кривошипы О1А и О2D действуют пары сил с моментами M1 и М2.
Определить, чему равна при равновесии деформация λ пружины, и указать, растянута пружина или сжата. Значении всех заданных величин приведены в табл. Д9а для рис. 0—4 и в табл. Д9б для рис. 5—9, где Q выражено в ньютонах, а М, M1, М2 — в ньютоно-метрах.
Построение чертежа начинать со стержня, направление которого определяется углом α; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10, б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10. а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10,б, где одновременно иначе изображены направляющие).Дано: механизм находится под действием приложенных сил в равновесии. На ползун В действует сила упругости пружины. Кроме того. На ползун D действует сила Q, а на звено 1 — пара сил с моментом М.
М=240 Н•м, Q=260 Н, с=100 Н/смНайти: чему равна при равновесии деформация пружины и указать, растянута пружина или сжата.
1.00 $ В корзину -
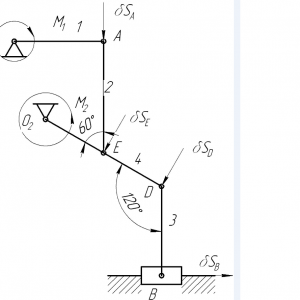
Тарг 1989 год задача Д9 вариант 33
Описание
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами α, β, γ, φ, θ (рис. Д9.0 — Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: l1=0,4 м, l4=0,6 м (размеры l2 и l3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины F, численно F = cλ, где с — коэффициент жесткости пружины, λ—ее деформация. Кроме того, на рис. 0 и 1 на ползун D действует сила Q, а на кривошип О1А — пара сил с моментом М; на рис. 2-9 на кривошипы О1А и О2D действуют пары сил с моментами M1 и М2.
Определить, чему равна при равновесии деформация λ пружины, и указать, растянута пружина или сжата. Значении всех заданных величин приведены в табл. Д9а для рис. 0—4 и в табл. Д9б для рис. 5—9, где Q выражено в ньютонах, а М, M1, М2 — в ньютоно-метрах.
Построение чертежа начинать со стержня, направление которого определяется углом α; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10, б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10. а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10,б, где одновременно иначе изображены направляющие).Дано: ℓ1=0,4 м, ℓ4=0,6 м , с=140 Н/см, М1=180 Н/м, М2=400 Н/м
1.00 $ В корзину
Найти: λ -
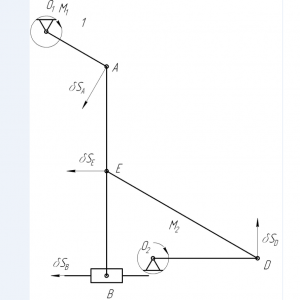
Тарг 1989 год задача Д9 вариант 63
Описание
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами α, β, γ, φ, θ (рис. Д9.0 — Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: l1=0,4 м, l4=0,6 м (размеры l2 и l3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины F, численно F = cλ, где с — коэффициент жесткости пружины, λ—ее деформация. Кроме того, на рис. 0 и 1 на ползун D действует сила Q, а на кривошип О1А — пара сил с моментом М; на рис. 2-9 на кривошипы О1А и О2D действуют пары сил с моментами M1 и М2.
Определить, чему равна при равновесии деформация λ пружины, и указать, растянута пружина или сжата. Значении всех заданных величин приведены в табл. Д9а для рис. 0—4 и в табл. Д9б для рис. 5—9, где Q выражено в ньютонах, а М, M1, М2 — в ньютоно-метрах.
Построение чертежа начинать со стержня, направление которого определяется углом α; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10, б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10. а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10,б, где одновременно иначе изображены направляющие).Дано: ℓ1=0,4 м, ℓ2=0,6 м , с=110 Н/см, М1=260 Н/м, М2=180 Н/м
Найти: λПояснения: В задаче Д9 поменяли углы, так как при данных варианта 63 всё равно 0 и нет решения
1.00 $ В корзину -

Тарг 1989 год задача Д9 вариант 66
Описание
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами α, β, γ, φ, θ (рис. Д9.0 — Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: l1=0,4 м, l4=0,6 м (размеры l2 и l3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины F, численно F = cλ, где с — коэффициент жесткости пружины, λ—ее деформация. Кроме того, на рис. 0 и 1 на ползун D действует сила Q, а на кривошип О1А — пара сил с моментом М; на рис. 2-9 на кривошипы О1А и О2D действуют пары сил с моментами M1 и М2.
Определить, чему равна при равновесии деформация λ пружины, и указать, растянута пружина или сжата. Значении всех заданных величин приведены в табл. Д9а для рис. 0—4 и в табл. Д9б для рис. 5—9, где Q выражено в ньютонах, а М, M1, М2 — в ньютоно-метрах.
Построение чертежа начинать со стержня, направление которого определяется углом α; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10, б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10. а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10,б, где одновременно иначе изображены направляющие).Дано: ℓ1=0,4 м, ℓ4=0,6 м , с=140 Н/см, М1=320 Н/м, М2=220 Н/м
1.00 $ В корзину
Найти: λ -
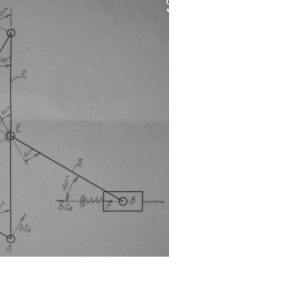
Тарг 1989 год задача Д9 вариант 73
Описание
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами α, β, γ, φ, θ (рис. Д9.0 — Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: l1=0,4 м, l4=0,6 м (размеры l2 и l3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины F, численно F = cλ, где с — коэффициент жесткости пружины, λ—ее деформация. Кроме того, на рис. 0 и 1 на ползун D действует сила Q, а на кривошип О1А — пара сил с моментом М; на рис. 2-9 на кривошипы О1А и О2D действуют пары сил с моментами M1 и М2.
Определить, чему равна при равновесии деформация λ пружины, и указать, растянута пружина или сжата. Значении всех заданных величин приведены в табл. Д9а для рис. 0—4 и в табл. Д9б для рис. 5—9, где Q выражено в ньютонах, а М, M1, М2 — в ньютоно-метрах.
Построение чертежа начинать со стержня, направление которого определяется углом α; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10, б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10. а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10,б, где одновременно иначе изображены направляющие).Найти: λ
1.00 $ В корзину -
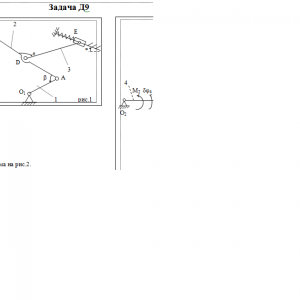
Тарг 1989 год задача Д9 вариант 79
Описание
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами α, β, γ, φ, θ (рис. Д9.0 — Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: l1=0,4 м, l4=0,6 м (размеры l2 и l3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины F, численно F = cλ, где с — коэффициент жесткости пружины, λ—ее деформация. Кроме того, на рис. 0 и 1 на ползун D действует сила Q, а на кривошип О1А — пара сил с моментом М; на рис. 2-9 на кривошипы О1А и О2D действуют пары сил с моментами M1 и М2.
Определить, чему равна при равновесии деформация λ пружины, и указать, растянута пружина или сжата. Значении всех заданных величин приведены в табл. Д9а для рис. 0—4 и в табл. Д9б для рис. 5—9, где Q выражено в ньютонах, а М, M1, М2 — в ньютоно-метрах.
Построение чертежа начинать со стержня, направление которого определяется углом α; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10, б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10. а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10,б, где одновременно иначе изображены направляющие).Дано: ℓ1=0,4 м, ℓ4=0,6 м , α=90°, β=150°, γ=120°, φ=90°, θ=30° с=180 Н/см, М1=380 Н/м, М2=160 Н/м
1.00 $ В корзину
Найти: λ -
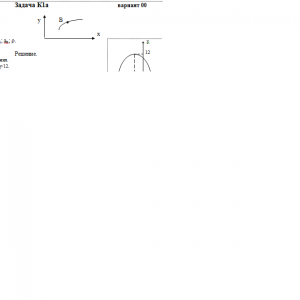
Тарг 1989 год задача К1 вариант 00
Описание
Под номером К1 помещены две задачи К1а и К16, которые надо решить.
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1(t), у= f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х= f1(t) указана непосредственно на рисунках, а зависимость у= f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1—С4, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. K1 — по последней.Дано: х=6*cos(πt/6)-3, y=12*sin(πt/6), t=1 c
Найти: уравнение траектории т.В; VB; aB; ρ.Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону s = f(t), заданному в табл. KI в столбце 5 (s — в метрах, t — в секундах), где s = АМ — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s — от А к М.
Дано: S= 4*cos(πt/6), R=2 м, S — дуга АМ, t=1 с
1.00 $ В корзину
Найти: V, а -
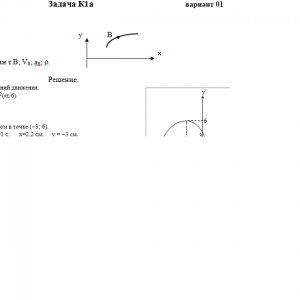
Тарг 1989 год задача К1 вариант 01
Описание
Под номером К1 помещены две задачи К1а и К16, которые надо решить.
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1(t), у= f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х= f1(t) указана непосредственно на рисунках, а зависимость у= f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1—С4, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. K1 — по последней.Дано: х=6*cos(πt/6)-3, y=-6*cos(πt/3), t=1 c
Найти: уравнение траектории т.В; VB; aB; ρ.Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону s = f(t), заданному в табл. KI в столбце 5 (s — в метрах, t — в секундах), где s = АМ — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s — от А к М.
Дано: S= 2*sin(πt/3), R=2 м, S — дуга АМ, t=1 с
1.00 $ В корзину
Найти: V, а -
Тарг 1989 год задача К1 вариант 02
Описание
Под номером К1 помещены две задачи К1а и К16, которые надо решить.
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1(t), у= f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
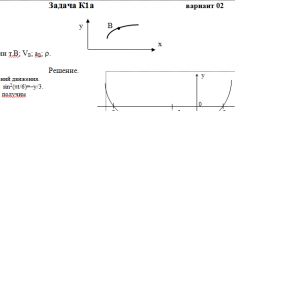
Зависимость х= f1(t) указана непосредственно на рисунках, а зависимость у= f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1—С4, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. K1 — по последней.Дано: х=6*cos(πt/6)-3, y=-3*sin2(πt/6), t=1 c
Найти: уравнение траектории т.В; VB; aB; ρ.Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону s = f(t), заданному в табл. KI в столбце 5 (s — в метрах, t — в секундах), где s = АМ — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s — от А к М.
Дано: S=6t-2t2, R=2 м, S — дуга АМ, t=1 с
1.00 $ В корзину
Найти: V, а -
Тарг 1989 год задача К1 вариант 03
Описание
Под номером К1 помещены две задачи К1а и К16, которые надо решить.
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1(t), у= f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
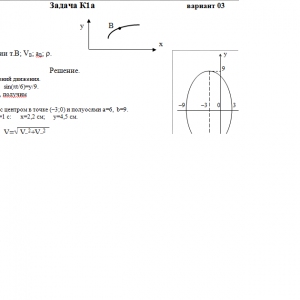
Зависимость х= f1(t) указана непосредственно на рисунках, а зависимость у= f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1—С4, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. K1 — по последней.Дано: х=6*cos(πt/6)-3, y=9*sin(πt/6), t=1 c
Найти: уравнение траектории т.В; VB; aB; ρ.Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону s = f(t), заданному в табл. KI в столбце 5 (s — в метрах, t — в секундах), где s = АМ — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s — от А к М.
Дано: S=-2*sin(πt/6), R=2 м, S — дуга АМ, t=1 с
1.00 $ В корзину
Найти: V, а -
Тарг 1989 год задача К1 вариант 04
Описание
Под номером К1 помещены две задачи К1а и К16, которые надо решить.
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1(t), у= f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
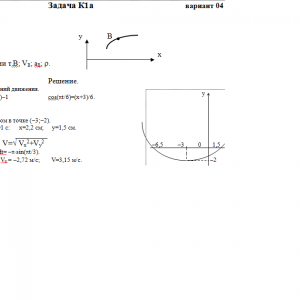
Зависимость х= f1(t) указана непосредственно на рисунках, а зависимость у= f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1—С4, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. K1 — по последней.Дано: х=6*cos(πt/6)-3, y=3*cos(πt/3), t=1 c
Найти: уравнение траектории т.В; VB; aB; ρ.Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону s = f(t), заданному в табл. KI в столбце 5 (s — в метрах, t — в секундах), где s = АМ — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s — от А к М.
Дано: S=4*cos(πt/3), R=2 м, S — дуга АМ, t=1 с
1.00 $ В корзину
Найти: V, а -
Тарг 1989 год задача К1 вариант 05
Описание
Под номером К1 помещены две задачи К1а и К16, которые надо решить.
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1(t), у= f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
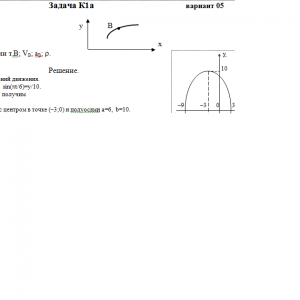
Зависимость х= f1(t) указана непосредственно на рисунках, а зависимость у= f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1—С4, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. K1 — по последней.Дано: х=6*cos(πt/6)-3, y=10*sin(πt/6), t=1 c
Найти: уравнение траектории т.В; VB; aB; ρ.Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону s = f(t), заданному в табл. KI в столбце 5 (s — в метрах, t — в секундах), где s = АМ — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s — от А к М.
Дано: S=-3*sin(πt/3), R=2 м, S — дуга АМ, t=1 с
1.00 $ В корзину
Найти: V, а -
Тарг 1989 год задача К1 вариант 06
Описание
Под номером К1 помещены две задачи К1а и К16, которые надо решить.
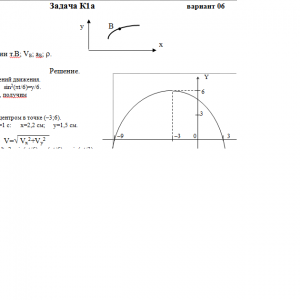
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1(t), у= f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х= f1(t) указана непосредственно на рисунках, а зависимость у= f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1—С4, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. K1 — по последней.Дано: х=6*cos(πt/6)-3, y=6*sin2(πt/6), t=1 c
Найти: уравнение траектории т.В; VB; aB; ρ.Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону s = f(t), заданному в табл. KI в столбце 5 (s — в метрах, t — в секундах), где s = АМ — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s — от А к М.
Дано: S=3*t2-10t, R=2 м, S — дуга АМ, t=1 с
1.00 $ В корзину
Найти: V, а -
Тарг 1989 год задача К1 вариант 07
Описание
Под номером К1 помещены две задачи К1а и К16, которые надо решить.
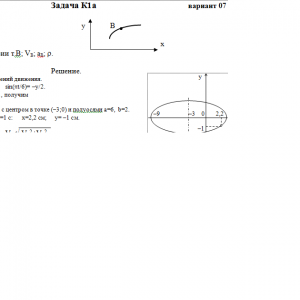
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1(t), у= f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х= f1(t) указана непосредственно на рисунках, а зависимость у= f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1—С4, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. K1 — по последней.Дано: х=6*cos(πt/6)-3, y=-2*sin(πt/6), t=1 c
Найти: уравнение траектории т.В; VB; aB; ρ.Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону s = f(t), заданному в табл. KI в столбце 5 (s — в метрах, t — в секундах), где s = АМ — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s — от А к М.
Дано: S=-2*cos(πt/3), R=2 м, S — дуга АМ, t=1 с
1.00 $ В корзину
Найти: V, а -
Тарг 1989 год задача К1 вариант 08
Описание
Под номером К1 помещены две задачи К1а и К16, которые надо решить.
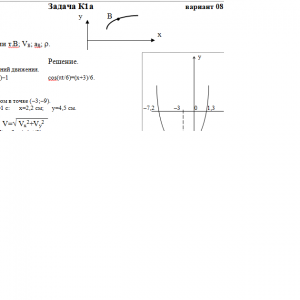
Задача К1а. Точка В движется в плоскости ху (рис. К1.0 — К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями: х = f1(t), у= f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х= f1(t) указана непосредственно на рисунках, а зависимость у= f2(t) дана в табл. К1 (для рис. 0-2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах С1—С4, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. K1 — по последней.Дано: х=6*cos(πt/6)-3, y=9*cos(πt/3), t=1 c
Найти: уравнение траектории т.В; VB; aB; ρ.Задача К1б. Точка движется по дуге окружности радиуса R = 2 м по закону s = f(t), заданному в табл. KI в столбце 5 (s — в метрах, t — в секундах), где s = АМ — расстояние точки от некоторого начала А, измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени t1 = 1 с. Изобразить на рисунке векторы v и а, считая, что точка в этот момент находится в положении М, а положительное направление отсчета s — от А к М.
Дано: S=3*sin(πt/6), R=2 м, S — дуга АМ, t=1 с
1.00 $ В корзину
Найти: V, а