Теоретическая механика методичка Тарга 1989
Отображение 641–672 из 1113
-
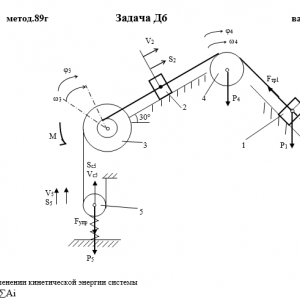
Тарг 1989 год задача Д6 вариант 81
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=8 кг, m2=0 кг, m3=0 кг, m4=4 кг, m5=6 кг, М=0,8 Н*м, C=320 Н/м, F=50*(8+3*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
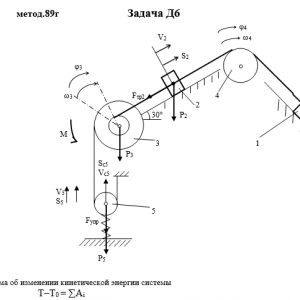
Тарг 1989 год задача Д6 вариант 82
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=4 кг, m3=6 кг, m4=0 кг, m5=5 кг, М=1,4 Н*м, C=240 Н/м, F=60*(6+5*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
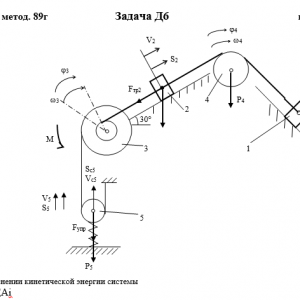
Тарг 1989 год задача Д6 вариант 83
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=6 кг, m3=0 кг, m4=5 кг, m5=4 кг, М=1,8 Н*м, C=300 Н/м, F=80*(5+6*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
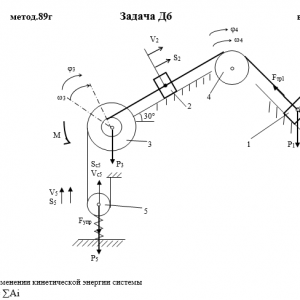
Тарг 1989 год задача Д6 вариант 84
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=5 кг, m2=0 кг, m3=4 кг, m4=0 кг, m5=6 кг, М=1,2 Н*м, C=240 Н/м, F=40*(9+4*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
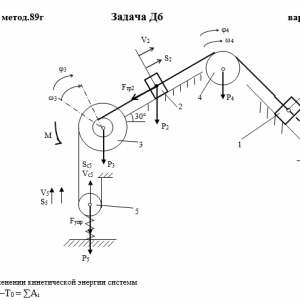
Тарг 1989 год задача Д6 вариант 85
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=5 кг, m3=0 кг, m4=6 кг, m5=4 кг, М=1,6 Н*м, C=280 Н/м, F=50*(7+8*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
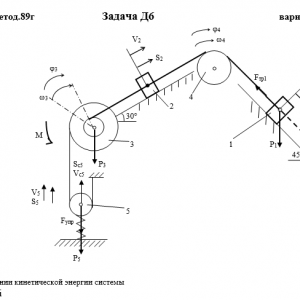
Тарг 1989 год задача Д6 вариант 86
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=8 кг, m2=0 кг, m3=5 кг, m4=0 кг, m5=6 кг, М=0,8 Н*м, C=280 Н/м, F=40*(8+9*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
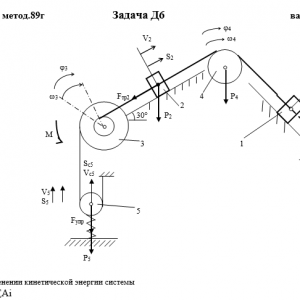
Тарг 1989 год задача Д6 вариант 87
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=4 кг, m3=0 кг, m4=6 кг, m5=5 кг, М=1,5 Н*м, C=300 Н/м, F=60*(8+5*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
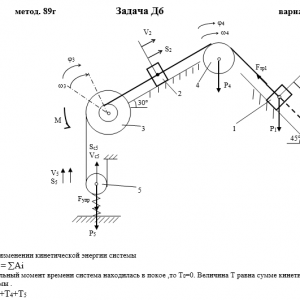
Тарг 1989 год задача Д6 вариант 88
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=4 кг, m2=0 кг, m3=0 кг, m4=5 кг, m5=6 кг, М=1,4 Н*м, C=320 Н/м, F=50*(9+2*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
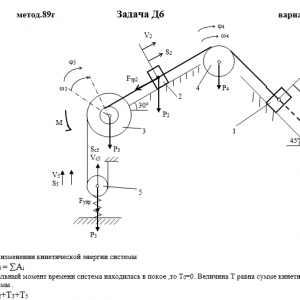
Тарг 1989 год задача Д6 вариант 89
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=5 кг, m3=6 кг, m4=0 кг, m5=4 кг, М=1,6 Н*м, C=280 Н/м, F=80*(6+7*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
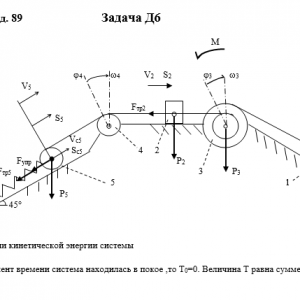
Тарг 1989 год задача Д6 вариант 90
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=6 кг, m3=4 кг, m4=0 кг, m5=5 кг, М=1,2 Н*м, C=200 Н/м, F=80*(4+5*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
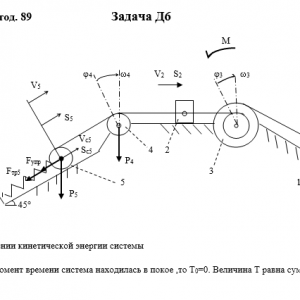
Тарг 1989 год задача Д6 вариант 91
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=8 кг, m2=0 кг, m3=0 кг, m4=4 кг, m5=6 кг, М=0,8 Н*м, C=320 Н/м, F=50*(8+3*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
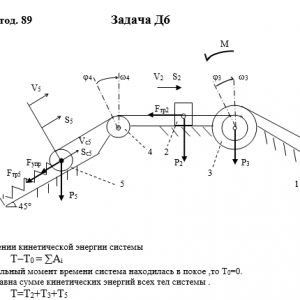
Тарг 1989 год задача Д6 вариант 92
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=4 кг, m3=6 кг, m4=0 кг, m5=5 кг, М=1,4 Н*м, C=240 Н/м, F=60*(6+5*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
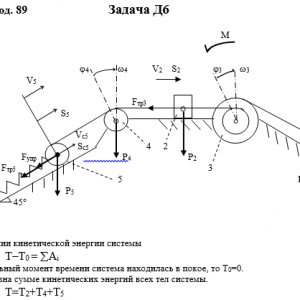
Тарг 1989 год задача Д6 вариант 93
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=6 кг, m3=0 кг, m4=5 кг, m5=4 кг, М=1,9 Н*м, C=300 Н/м, F=80*(5+6*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
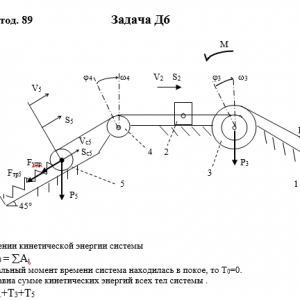
Тарг 1989 год задача Д6 вариант 94
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=5 кг, m2=0 кг, m3=4 кг, m4=0 кг, m5=6 кг, М=1,2 Н*м, C=320 Н/м, F=40*(9+4*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
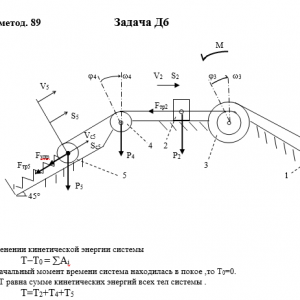
Тарг 1989 год задача Д6 вариант 95
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=5 кг, m3=0 кг, m4=6 кг, m5=4 кг, М=1,6 Н*м, C=200 Н/м, F=50*(7+8*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
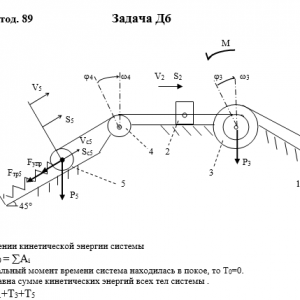
Тарг 1989 год задача Д6 вариант 96
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=8 кг, m2=0 кг, m3=6 кг, m4=0 кг, m5=5 кг, М=0,8 Н*м, C=280 Н/м, F=40*(8+9*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
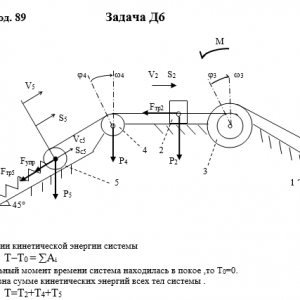
Тарг 1989 год задача Д6 вариант 97
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=4 кг, m3=0 кг, m4=6 кг, m5=5 кг, М=1,5 Н*м, C=300 Н/м, F=60*(8+5*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
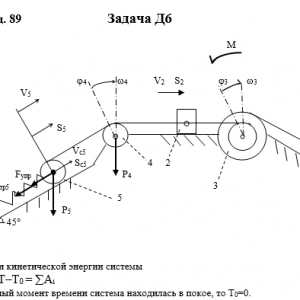
Тарг 1989 год задача Д6 вариант 98
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=4 кг, m2=0 кг, m3=0 кг, m4=5 кг, m5=6 кг, М=1,4 Н*м, C=320 Н/м, F=50*(9+2*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -
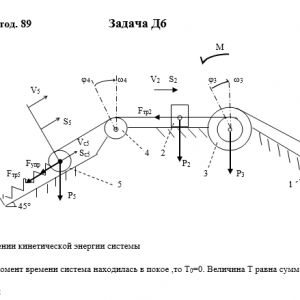
Тарг 1989 год задача Д6 вариант 99
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3=0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2 м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д6.0 — Д6.9, табл. Дб); тело 5 считать сплошным однородным цилиндром, а массу блока 4 — равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vc5 — скорости грузов 1,2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 2), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2 = 0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=5 кг, m3=6 кг, m4=0 кг, m5=4 кг, М=1,6 Н*м, C=280 Н/м, F=80*(6+7*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1, S1=0,2 м
1.00 $ В корзину
Найти: ω4 -

Тарг 1989 год задача Д7 вариант 33
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: α=30°, М=0,4РR
1.00 $ В корзину
Найти: Закон движения барабана, Наименьший коэффициент трения fmin, при котором возможно качение без скольжения. -

Тарг 1989 год задача Д7 вариант 55
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: α=0, F1=0,3P, F2=0,1P.
1.00 $ В корзину
Найти: Закон движения барабана, Наименьший коэффициент трения fmin, при котором возможно качение без скольжения. -
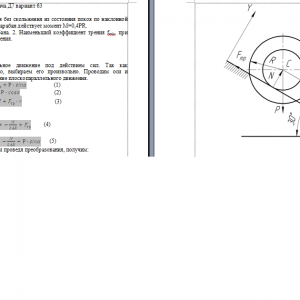
Тарг 1989 год задача Д7 вариант 63
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: α=30°, М=0,4РR
1.00 $ В корзину
Найти: Закон движения барабана, Наименьший коэффициент трения fmin, при котором возможно качение без скольжения. -

Тарг 1989 год задача Д7 вариант 66
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: F2=0,3P, М=0,2РR, r=0,6R
1.00 $ В корзину
Найти: Закон движения барабана, Наименьший коэффициент трения fmin, при котором возможно качение без скольжения. -

Тарг 1989 год задача Д7 вариант 75
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: F1=0,3P, F2=0,1P, α=0°
1.00 $ В корзину
Найти: Закон движения барабана, Наименьший коэффициент трения fmin, при котором возможно качение без скольжения. -

Тарг 1989 год задача Д7 вариант 78
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: r =0,6*R, α=30° β=90°, F1 = 0, F2 = 0,2P, M = -0,4*PR
1.00 $ В корзину
Найти: Xc(t), fmin -
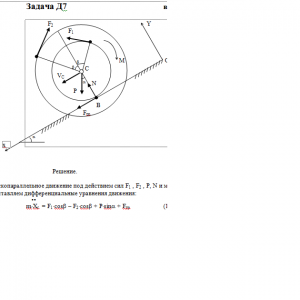
Тарг 1989 год задача Д7 вариант 85
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: r =0,6*R, α=0° β=60°, F1 = 0,3P, F2 = 0,1P, M = 0
1.00 $ В корзину
Найти: Xc(t), fmin -
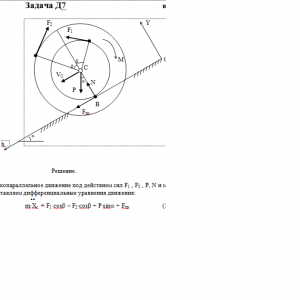
Тарг 1989 год задача Д7 вариант 89
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: r =0,6*R, α=30° β=210°, F1 = 0,1P, F2 = 0, M = -0,3*PR
1.00 $ В корзину
Найти: Xc(t), fmin -

Тарг 1989 год задача Д8 вариант 00
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, α=45°, β=135°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RВ -

Тарг 1989 год задача Д8 вариант 01
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, α=60°, β=240°, φ=45°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RК -

Тарг 1989 год задача Д8 вариант 02
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, α=30°, β=210°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RК -

Тарг 1989 год задача Д8 вариант 03
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, α=60°, β=150°, φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RD -

Тарг 1989 год задача Д8 вариант 04
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, α=30°, β=120°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RВ