Описание
Задача 4
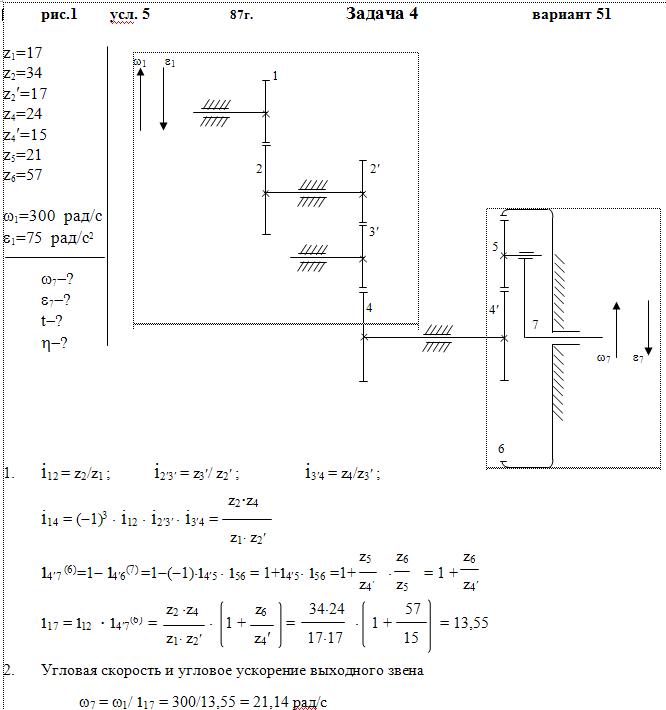
1) На рис. 4, 1-Х показаны схемы зубчатых передач. Входное колесо 1 в данный момент имеет угловую скорость ω1 и постоянное угловое ускорение ε1 направленное по движению или против движения.
Определить:
1) передаточное отношение между входным и выходном звеньями и его знак (если их оси вращения параллельны);
2) угловую скорость и угловое ускорение выходного звена, их направления показать на схеме передачи;
3) время, в течение которого угловая скорость увеличится в два раза (если движение ускоренное), или уменьшится до нуля (если движение замедленное);
4) общий коэффициент полезного действия передачи,
В таблице заданных величин z-число зубьев колес приводится с индексом, соответствующим их номеру на схеме механизма, для червяка z-число заходов, а направление витков червяка указано буквами: л-левое, п-правое.
Для расчетов принять следующие значения к. п, д. (учитывающего потери и в зацеплении, и в подшипниках): для пары цилиндрических колес ηц=0,97; для пары конических колес ηк=0,95; для планетарной передачи с внешними зацеплениями ее колес ηп=0,5, а для имеющей внутреннее зацепление одной из пар ηв=0,96; для червячной передачи при одно-, двух- и трехзаходном червяке — соответственно ηч=0,7; 0,75; 0,8.
Для решения задачи нужно определить, из каких видов передач состоит заданное сложное соединение зубчатых колес, уметь находить планетарную передачу с ее характерными звеньями водилом и сателлитами, разделить передачи на плоские и пространственные (с непараллельными осями вращения). Нужно понимать, когда направления вращений можно определять по алгебраическим знакам передаточного отношения, а когда для этого применять простановку стрелок на схеме. На червяк схематично нанести витки соответственно заданному направлению и учитывать его при определении направлений вращения. Очень важны показанные направления угловой скорости и углового ускорения — по ним определяют характер движения (ускоренное, замедленное)
Методичка по прикладной механике и механике
Методичка Преображенский 1987г. Москва