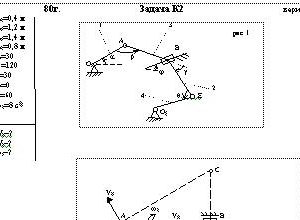
Описание
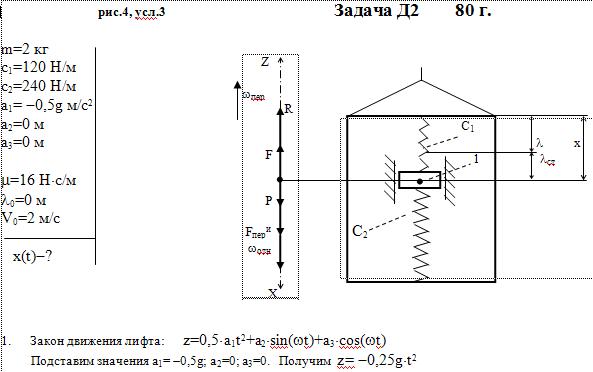
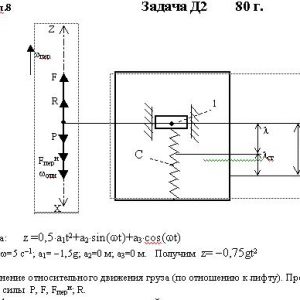
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону
z =1/2*a1t2+a2*sin(ωt)+a3*cos(ωt)
(ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R =μv, где v— скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т.е. х = f(t): начало координат поместить в положении статического равновесия груза при неподвижном лифте. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3—коэффициенты жесткости пружин, λст— статическое удлинение пружины с эквивалентной жесткостью, λ0 — удлинение пружины с эквивалентной жесткостью в начальный момент времени t0= 0, v0—начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк во всех столбцах с1 с2, с3 стоит, когда задано λст (пружину с эквивалентной жесткостью считать в этом случае прикрепленной к потолку лифта), а прочерк в одном из столбцов означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин. Условие μ = 0 означает, что сила сопротивления R отсутствует.
Дано: m=2 кг, с1=120 Н/м, с2=240 Н/м, a1= -0,5g м/с2, a2=0 м, a3=0 м, μ=16 Н*с/м, λ0=0 м, V0=2 м/с,
Найти: x(t)