Описание
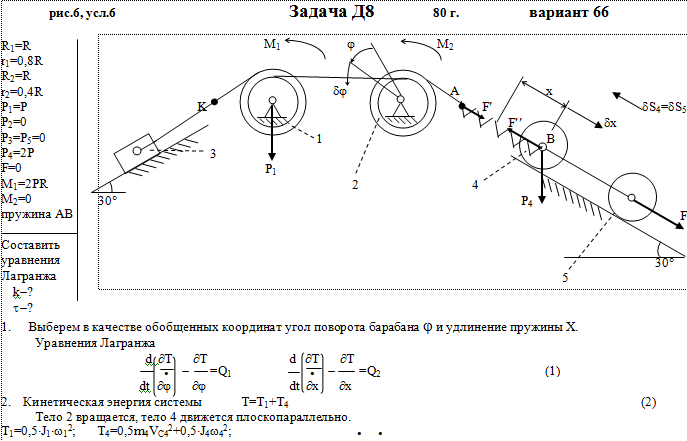
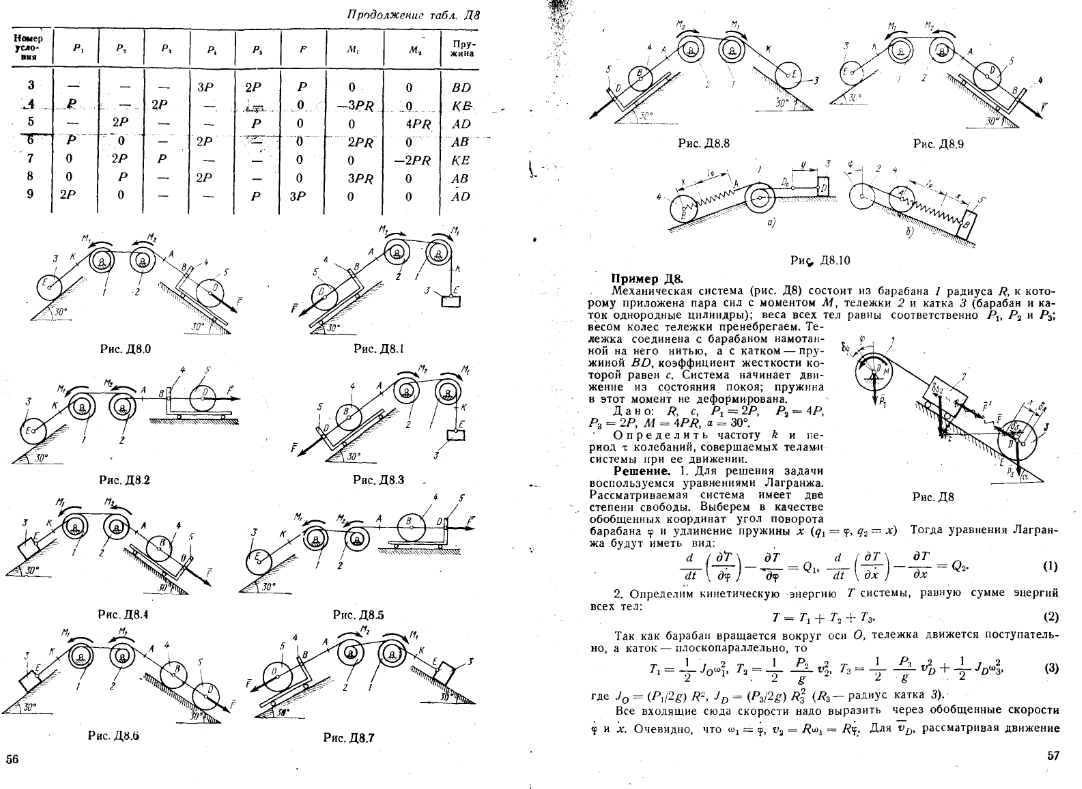
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке.
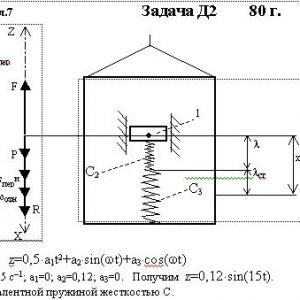
На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы.
Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении.
Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4.
Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=P5=0, P4=2P, F=0, M1=2PR, M2=0, пружина AB
Найти: Составить уравнения Лагранжа, k-?, τ-?