Описание
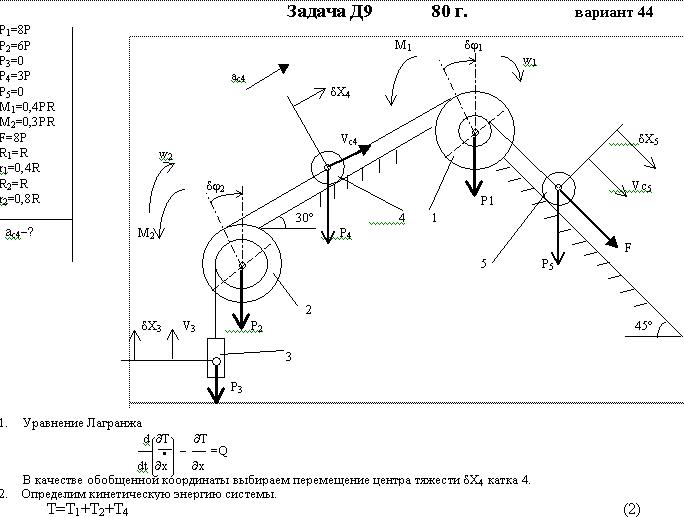
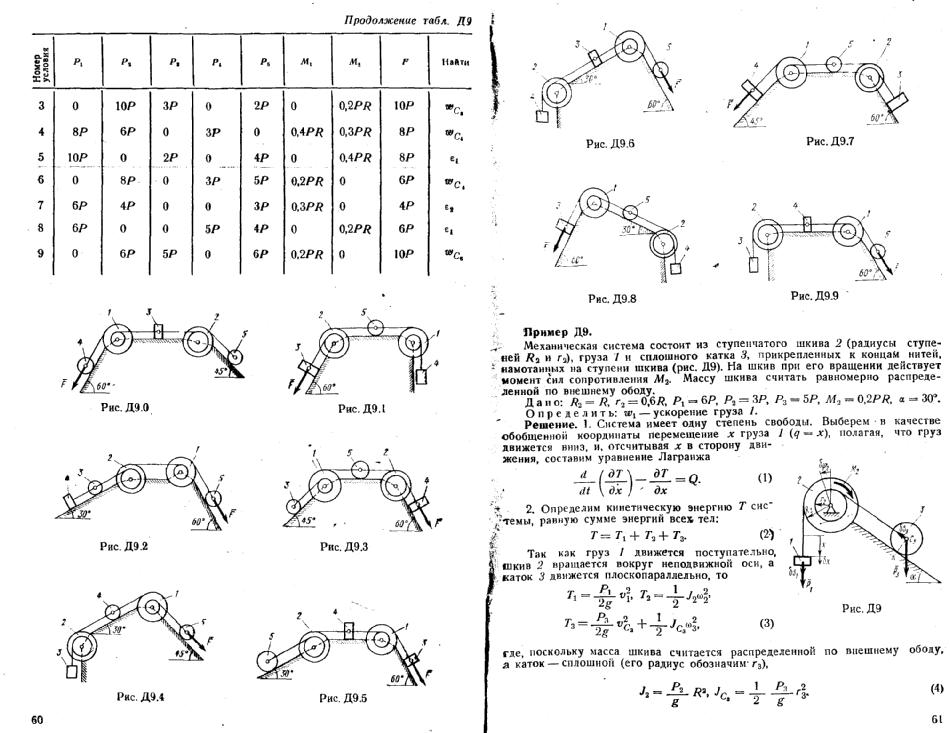
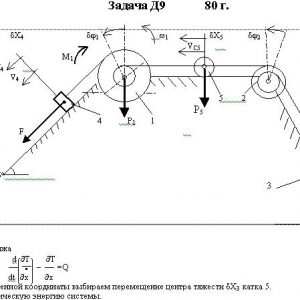
Механическая система состоит из ступенчатых шкивов 1 и 2 весом Р1 и Р2 с радиусами ступеней R1 = R, r1 = 0,4R, R2 = R, r2 = 0,8R (массу каждого шкива считать равномерно распределенной по его внешнему ободу) и грузов или сплошных однородных цилиндрических катков 3, 4, 5 весом Р3, P4, Р5 соответственно (рис. Д9.0 —Д9.9, табл. Д9). Тела системы соединены нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Грузы скользят по плоскостям без трения, а катки катятся без скольжения.
Кроме сил тяжести на одно из тел системы действует постоянная сила F, а на шкивы 1 и 2 при их вращении действуют постоянные моменты сил сопротивления, равные соответственно М1 и М2.
Составить для данной системы уравнение Лагранжа и определить из него величину, указанную в таблице в столбце Найти, где обозначено: ε1, ε2 — угловые ускорения шкивов 1 и 2, аC3, аC4, аC5 — ускорения центров масс тел 3, 4, 5 (если тело 3 или 4 — груз, то аСз = а3, аС4 = а4, где а3 и а4 — ускорения соответствующих грузов). Когда в задаче надо определить ε1 или ε2, считать R = 0,25 м.
То из тел 3, 4, вес которого равен нулю, на чертеже не изображать. Шкивы 1 и 2 всегда входят в систему.
Дано: P1=8P, P2=6P, P3=0, P4=3P, P5=0, М1=0,4PR, M2=0,3PR, F=8P, R1=R, r1=0,4R, R2=R, r2=0,8R
Найти: aC4