Описание
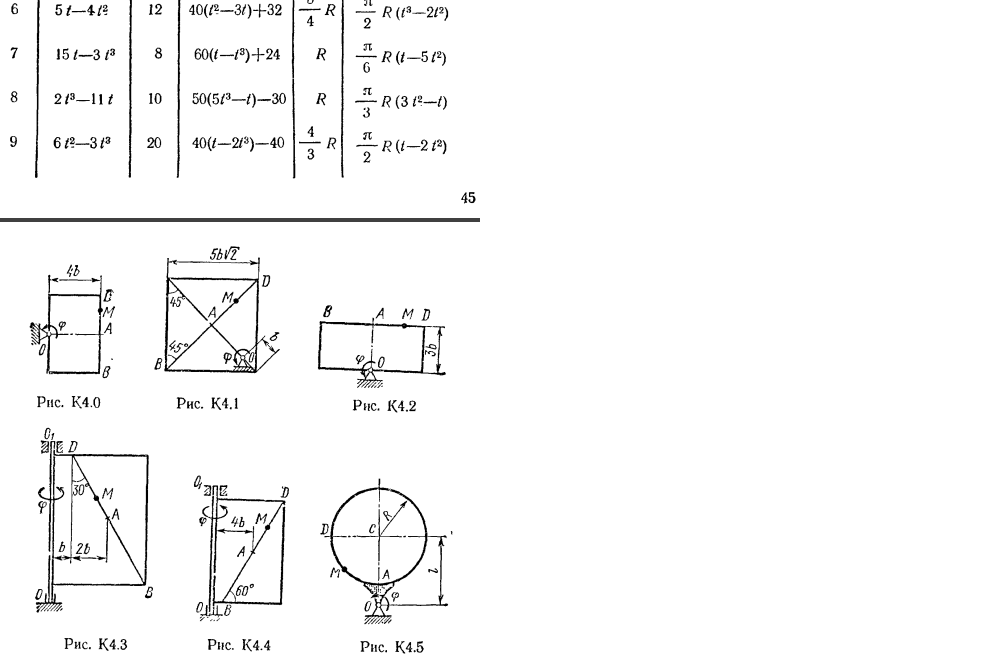
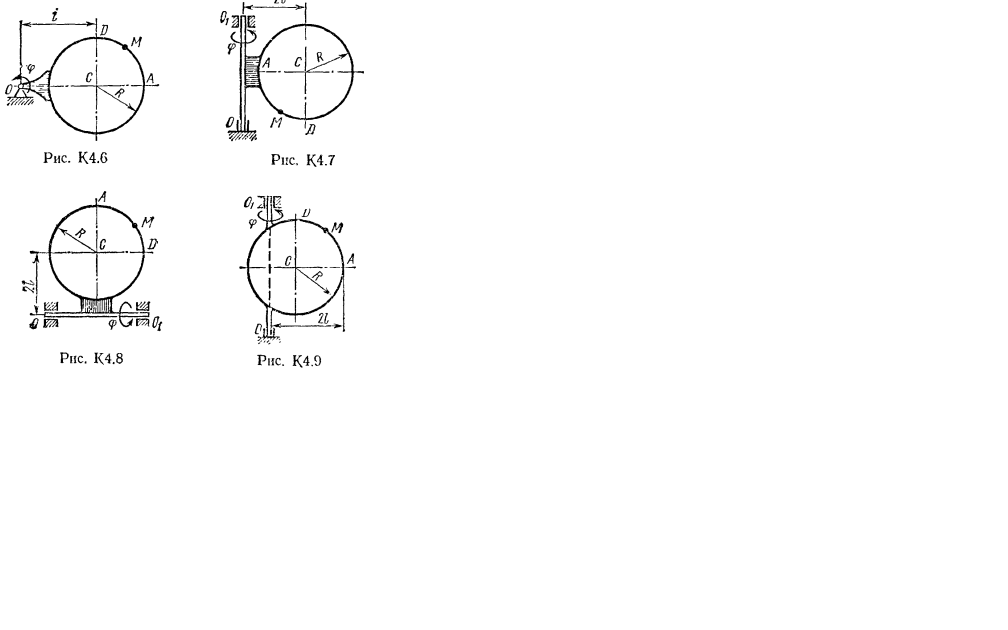
Прямоугольная пластина (рис. К4.0—К4.4) или круглая пластина радиуса R=60 см (рис. К4.5—К4.9) вращается вокруг неподвижной оси но закону φ=f1(t) заданному в табл. К4. Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. На рис. О, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения OO1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. О—4) или по окружности радиуса R (рис. 5—9) движется точка М; закон ее относительного движения, т. е. зависимость s=AM=f2(t) (s выражено в сантиметрах, t—в секундах), задан в таблице отдельно для рис. 0—4 и для рис. 5—9; там же даны размеры b и l. На рисунках точка М показана в положении, при котором s=AM>0 (при s<0 точка М находится по другую сторону от точки А).
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 с.
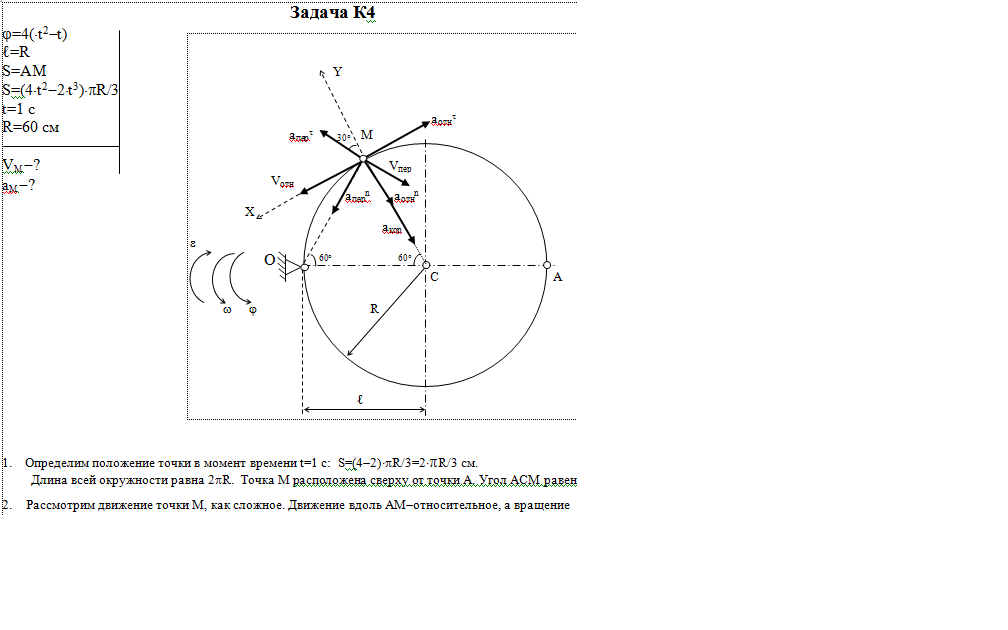
Дано: φ=4(t2-t), ℓ=R, S=AM, S=(4*t2-t3)*πR/3, t=1 c, R=60 см
Найти: VM, aM