Описание
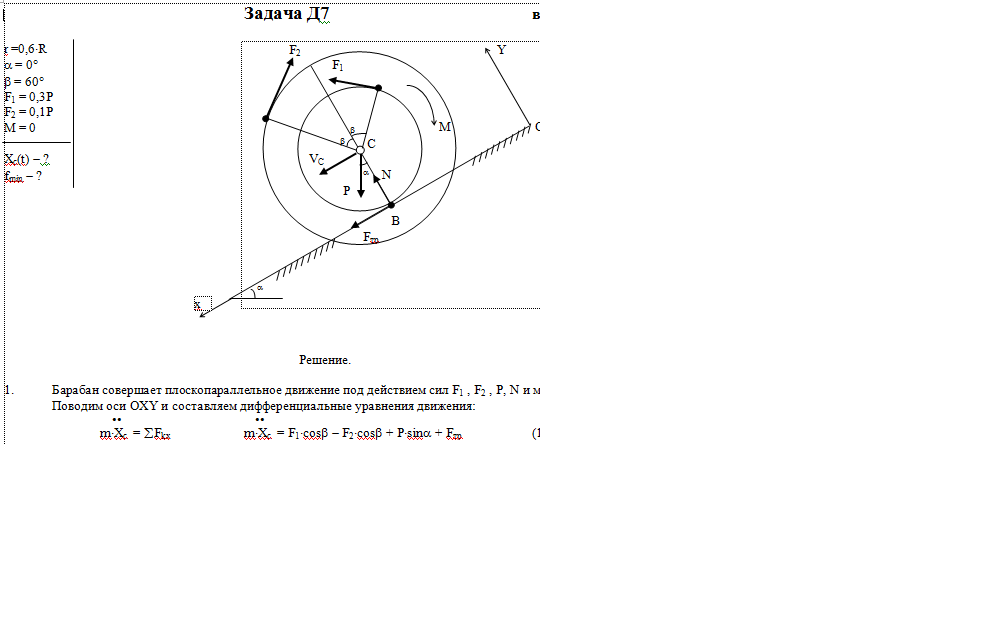
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.
Дано: r =0,6*R, α=0° β=60°, F1 = 0,3P, F2 = 0,1P, M = 0
Найти: Xc(t), fmin