Описание
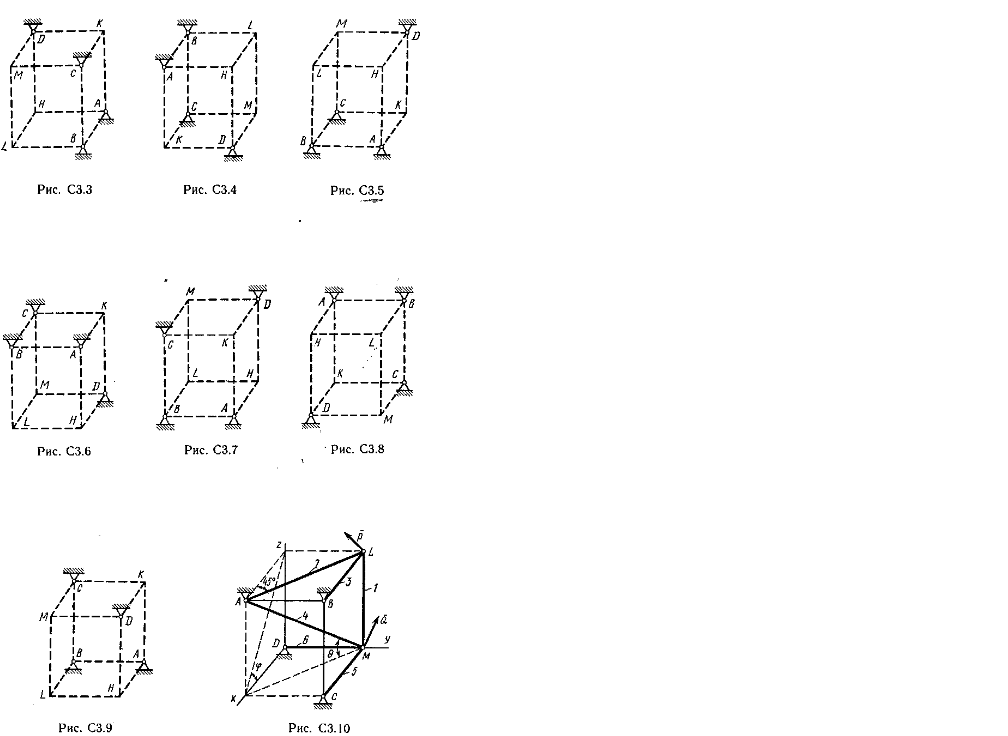
Шесть невесомых стержней соединены своими концами шарнирно друг с другом в двух узлах и прикреплены другими концами (тоже шарнирно) к неподвижным опорам
A, B, C, D (рис. СЗ.О — С3.9, табл. СЗ). Стержни и узлы (узлы расположены в вершинах H, K, L или M прямоугольного параллелепипеда) на рисунках не показаны
и должны быть изображены решающим задачу по данным таблицы. В узле, который в каждом столбце таблицы указан первым, приложена сила P = 200 Н; во втором
узле приложена сила Q = 100 Н. Сила P образует с положительными направлениями координатных осей x, y, z углы, равные соответственно
α1 = 45°, β1 = 60°, γ1 = 60°, а сила Q — углы α2 = 60°, β2 = 45°, γ2 = 60°; направления осей x, y, z для всех рисунков показаны на рис. СЗ.О.
Грани параллелепипеда, параллельные плоскости xy, — квадраты. Диагонали других боковых граней образуют с плоскостью xy угол φ = 60°,
а диагональ параллелепипеда образует с этой плоскостью угол θ = 51°. Определить усилия в стержнях.
На рис. С3.10 в качестве примера показано, как должен выглядеть чертеж С3.1, если по условиям задачи узлы находятся в точках L и M, а стержнями являются
LM, LA, LB, MA, MC, MD. Там же показаны углы φ и θ.
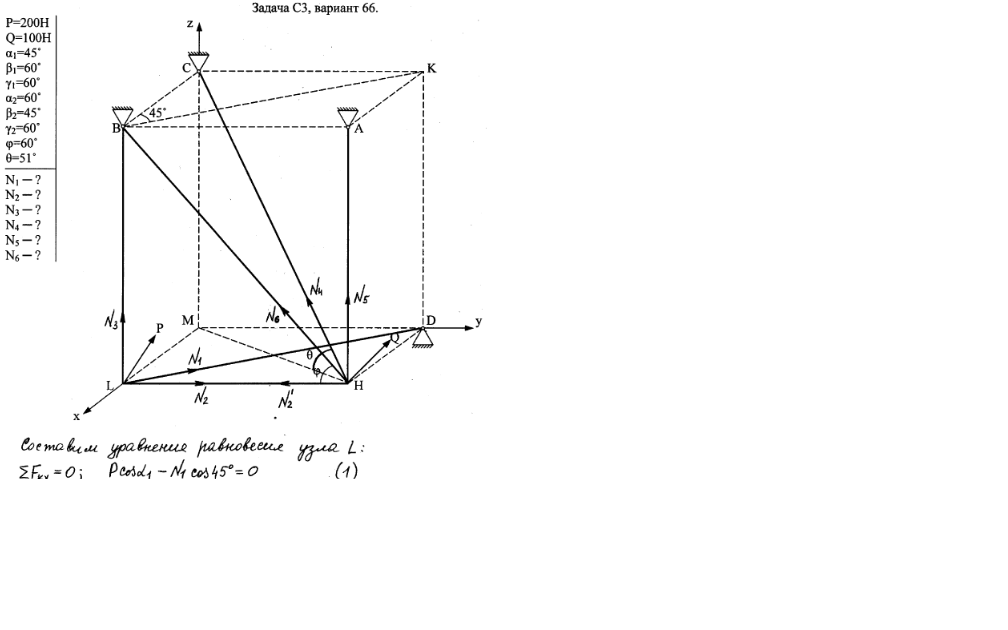
Дано: P=200 H, Q=100 H, α1=45°, β1=60°, γ1=60°, α2=60°, β2=45°, γ2=60°, φ=60°, θ=51°
Найти: усилия в стержнях
Указания. Задача СЗ — на равновесие пространственной системы сходящихся сил. При ее решении следует рассмотреть отдельно равновесие каждого из двух узлов, где сходятся стержни и приложены заданные силы, и учесть закон о равенстве действия и противодействия; начинать с узла, где сходятся три стержня.
Изображать чертеж можно без соблюдения масштаба так, чтобы лучше были видны все шесть стержней. Стержни следует пронумеровать в том порядке, в каком они указаны в таблице; реакции стержней обозначать буквой с индексом, соответствующим номеру стержня (например, N1, N2 и т.д.).