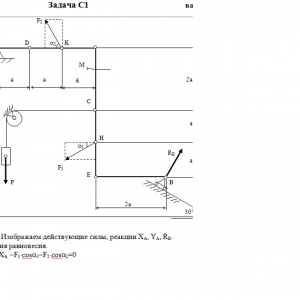
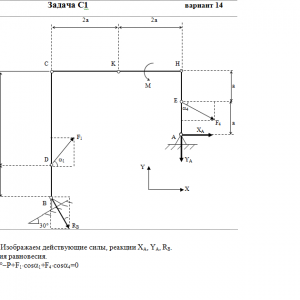
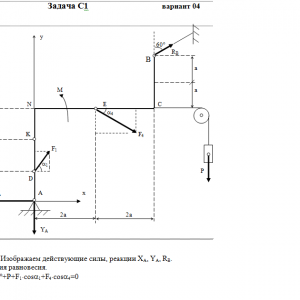
Описание
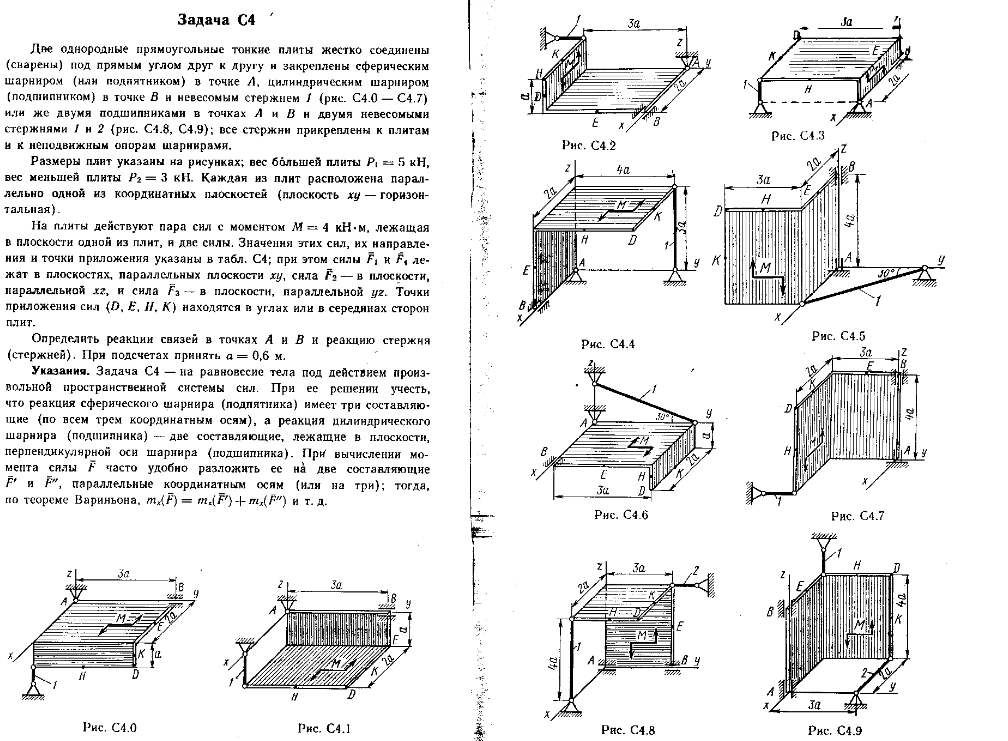
Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром (или подпятником)в точке A, цилиндрическим шарниром (подшипником) в точке В и невесомым стержнем 1 (рис. С4.0 — С4.7) или же двумя подшипниками в точках A и В и двумя невесомыми стержнями 1 и 2 (рис. С4.8, С4.9); все стержни прикреплены к плитам и к неподвижным опорам шарнирами.
Размеры плит указаны на рисунках; вес большей плиты Р1 = 5 кН, вес меньшей плиты Р2 = 3 кН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость xy — горизонтальная).
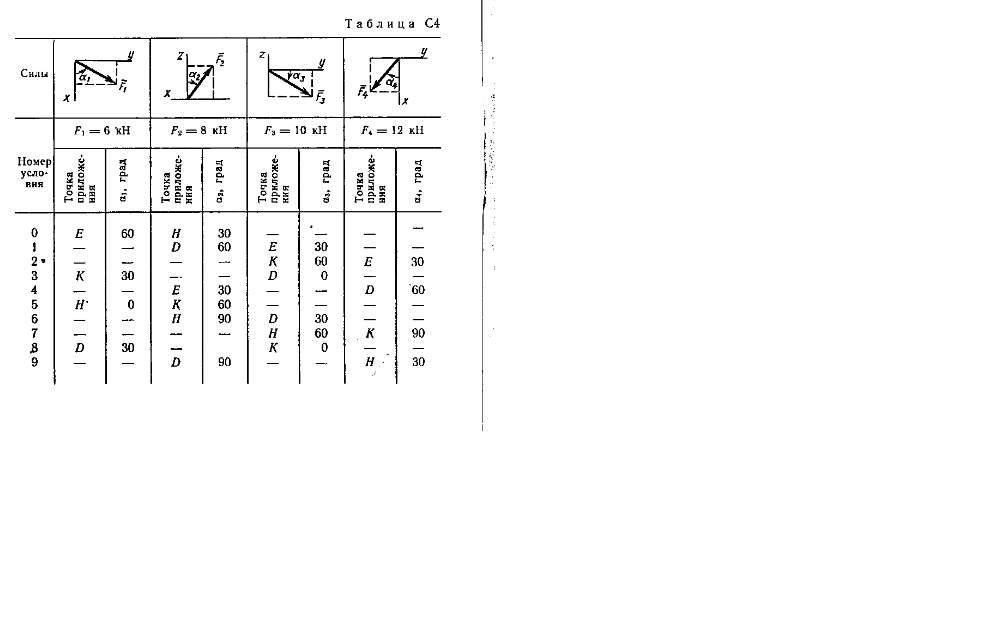
На плиты действуют пара сил с моментом М = 4 кН*м, лежащая в плоскости одной из плит, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С4; при этом силы F1 и F4 лежат в плоскостях, параллельных плоскости xy, сила F2 — в плоскости, параллельной xz, и сила F3 — в плоскости, параллельной yz. Точки приложения сил (D, E, H, K) находятся в углах или в серединах сторон плит.
Определить реакции связей в точках А и В и реакцию стержня (стержней). При подсчетах принять а = 0,6 м.
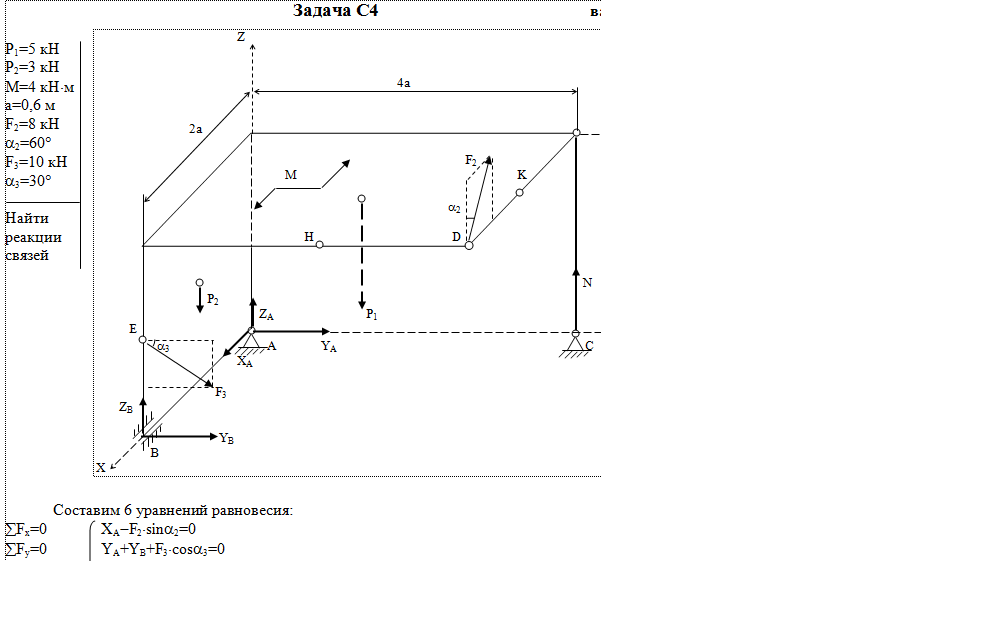
Дано: P1=5 кН, P2=3 кН, M=4 кН*м, a=0,6 м, F2=8 кН, α2=60°, F3=10 кН, α3=30°
Найти: Найти реакции связей
Указания. Задача С4 — на равновесие тела под действием произвольной пространственной системы сил. При ее решении учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) — две составляющие, лежащие в плоскости, перпендикулярной оси шарнира (подшипника). При вычислении момента силы F часто удобно разложить ее на две составляющие F‘ и F‘‘, параллельные координатным осям (или на три); тогда, по теореме Вариньона, mx(F) = mx((F‘) + mx(F‘‘) и т.д.