Магазин
Отображение 2689–2720 из 3934
-

Тарг 1989 год задача Д7 вариант 55
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: α=0, F1=0,3P, F2=0,1P.
1.00 $ В корзину
Найти: Закон движения барабана, Наименьший коэффициент трения fmin, при котором возможно качение без скольжения. -
Тарг 1989 год задача Д7 вариант 63
Описание
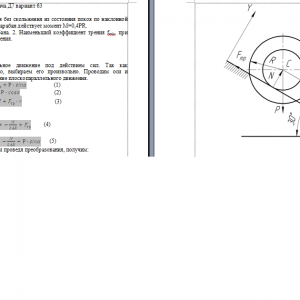
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: α=30°, М=0,4РR
1.00 $ В корзину
Найти: Закон движения барабана, Наименьший коэффициент трения fmin, при котором возможно качение без скольжения. -

Тарг 1989 год задача Д7 вариант 66
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: F2=0,3P, М=0,2РR, r=0,6R
1.00 $ В корзину
Найти: Закон движения барабана, Наименьший коэффициент трения fmin, при котором возможно качение без скольжения. -

Тарг 1989 год задача Д7 вариант 75
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: F1=0,3P, F2=0,1P, α=0°
1.00 $ В корзину
Найти: Закон движения барабана, Наименьший коэффициент трения fmin, при котором возможно качение без скольжения. -

Тарг 1989 год задача Д7 вариант 78
Описание
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: r =0,6*R, α=30° β=90°, F1 = 0, F2 = 0,2P, M = -0,4*PR
1.00 $ В корзину
Найти: Xc(t), fmin -
Тарг 1989 год задача Д7 вариант 85
Описание
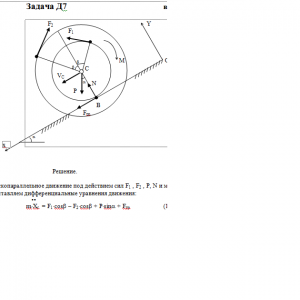
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: r =0,6*R, α=0° β=60°, F1 = 0,3P, F2 = 0,1P, M = 0
1.00 $ В корзину
Найти: Xc(t), fmin -
Тарг 1989 год задача Д7 вариант 89
Описание
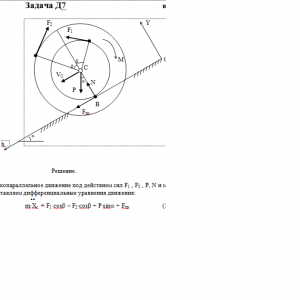
Барабан радиуса R весом Р имеет выточку (как у катушки) радиуса r = 0,6R (рис. Д7.0-Д7.9, табл. Д7). К концам намотанных на барабан нитей приложены постоянные силы F1 и F2, направления которых определяются углом β; кроме сил на барабан действует пара с моментом М, когда в таблице М<0, направление момента противоположно показанному на рисунке. При движении, начинающемся из состояния покои, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс С барабана, т. е. хс = f(t), и наименьшее значение коэффициента трения f о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.Дано: r =0,6*R, α=30° β=210°, F1 = 0,1P, F2 = 0, M = -0,3*PR
1.00 $ В корзину
Найти: Xc(t), fmin -

Тарг 1989 год задача Д8 вариант 00
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, α=45°, β=135°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RВ -

Тарг 1989 год задача Д8 вариант 01
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, α=60°, β=240°, φ=45°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RК -

Тарг 1989 год задача Д8 вариант 02
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, α=30°, β=210°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RК -

Тарг 1989 год задача Д8 вариант 03
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, α=60°, β=150°, φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RD -

Тарг 1989 год задача Д8 вариант 04
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, α=30°, β=120°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RВ -
Тарг 1989 год задача Д8 вариант 05
Описание
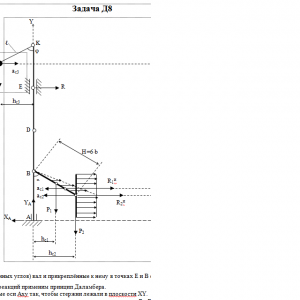
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=45°, β=225°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -

Тарг 1989 год задача Д8 вариант 06
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=60°, φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RЕ -
Тарг 1989 год задача Д8 вариант 07
Описание
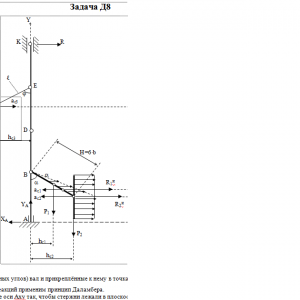
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, β=30°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -

Тарг 1989 год задача Д8 вариант 08
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=150°, φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RD -

Тарг 1989 год задача Д8 вариант 09
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, β=120°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RЕ -

Тарг 1989 год задача Д8 вариант 10
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=45°, β=135°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -

Тарг 1989 год задача Д8 вариант 11
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=240°, φ=45°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RК -

Тарг 1989 год задача Д8 вариант 12
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, γ=210°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -

Тарг 1989 год задача Д8 вариант 13
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=150°, φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RD -

Тарг 1989 год задача Д8 вариант 14
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, β=120°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -

Тарг 1989 год задача Д8 вариант 15
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=45°, β=225°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RЕ -

Тарг 1989 год задача Д8 вариант 16
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=60°, φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RЕ -
Тарг 1989 год задача Д8 вариант 17
Описание
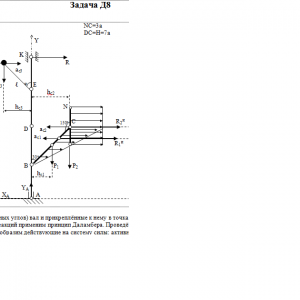
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, β=30°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -

Тарг 1989 год задача Д8 вариант 18
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=150°, φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RD -

Тарг 1989 год задача Д8 вариант 19
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, β=120°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RЕ -
Тарг 1989 год задача Д8 вариант 20
Описание
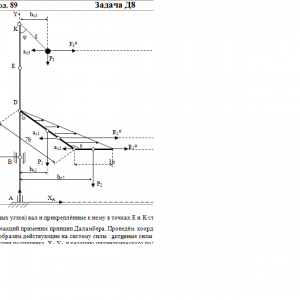
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=45°, β=135°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -

Тарг 1989 год задача Д8 вариант 21
Описание
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=240°, φ=45°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, RК -
Тарг 1989 год задача Д8 вариант 22
Описание
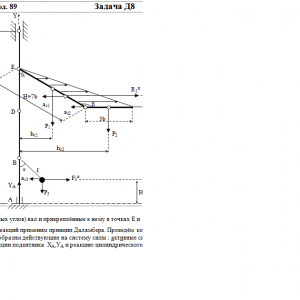
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=30°, β=210°, φ=60°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -
Тарг 1989 год задача Д8 вариант 23
Описание
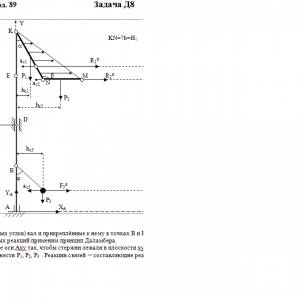
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=150°, φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R -
Тарг 1989 год задача Д8 вариант 28
Описание
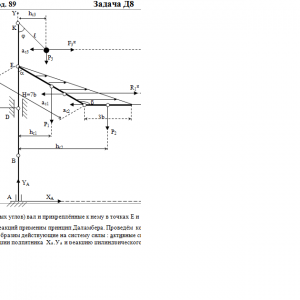
Вертикальный вал АК (рис. Д8.0 — Д8.9), вращающийся с постоянной угловой скоростью ω = 10 с-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в табл. Д8 в столбце 2 (АВ = BD = DЕ = ЕK=а). К валу жестко прикреплены тонкий однородный ломаный стержень массой m = 10 кг, состоящий из частей 1 и 2 (размеры частей стержня показаны на рисунках, где b=0,1м, а их массы m1 и m2 пропорциональны длинам), и невесомый стержень длиной ℓ=4b с точечкой массой m3 = 3 кг на конце; оба стержня лежат в одной плоскости. Точки крепления стержней указаны в таблице в столбцах 3 и 4, а углы α, β, γ, φ даны в столбцах 5—8.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять а = 0,6 м.Дано: m=10 кг, b=0,1 м, ℓ=4b, m3=3 кг, a=0,6 м, AB=BD=DE=EK=a, α=60°, β=150°, φ=30°, ω = 10 с-1
1.00 $ В корзину
Найти: XА, YА, R