Магазин
Отображение 3041–3072 из 3934
-
Тарг 1989 год задача С3 вариант 91
Описание
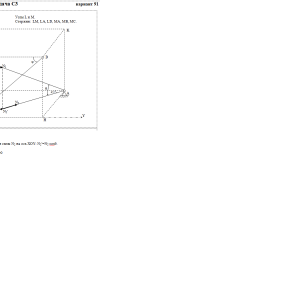
Шесть невесомых стержней соединены своими концами шарнирно друг с другом в двух узлах и прикреплены другими концами (тоже шарнирно) к неподвижным опорам
A, B, C, D (рис. СЗ.О — С3.9, табл. СЗ). Стержни и узлы (узлы расположены в вершинах H, K, L или M прямоугольного параллелепипеда) на рисунках не показаны
и должны быть изображены решающим задачу по данным таблицы. В узле, который в каждом столбце таблицы указан первым, приложена сила P = 200 Н; во втором
узле приложена сила Q = 100 Н. Сила P образует с положительными направлениями координатных осей x, y, z углы, равные соответственно
α1 = 45°, β1 = 60°, γ1 = 60°, а сила Q — углы α2 = 60°, β2 = 45°, γ2 = 60°; направления осей x, y, z для всех рисунков показаны на рис. СЗ.О.
Грани параллелепипеда, параллельные плоскости xy, — квадраты. Диагонали других боковых граней образуют с плоскостью xy угол φ = 60°,
а диагональ параллелепипеда образует с этой плоскостью угол θ = 51°. Определить усилия в стержнях.
На рис. С3.10 в качестве примера показано, как должен выглядеть чертеж С3.1, если по условиям задачи узлы находятся в точках L и M, а стержнями являются
LM, LA, LB, MA, MC, MD. Там же показаны углы φ и θ.Дано: P=200 H, Q=100 H, α1=45°, β1=60°, γ1=60°, α2=60°, β2=45°, γ2=60°, φ=60°, θ=51°
Найти: усилия в стержняхУказания. Задача СЗ — на равновесие пространственной системы сходящихся сил. При ее решении следует рассмотреть отдельно равновесие каждого из двух узлов, где сходятся стержни и приложены заданные силы, и учесть закон о равенстве действия и противодействия; начинать с узла, где сходятся три стержня.
1.00 $ В корзину
Изображать чертеж можно без соблюдения масштаба так, чтобы лучше были видны все шесть стержней. Стержни следует пронумеровать в том порядке, в каком они указаны в таблице; реакции стержней обозначать буквой с индексом, соответствующим номеру стержня (например, N1, N2 и т.д.). -
Тарг 1989 год задача С4 вариант 00
Описание
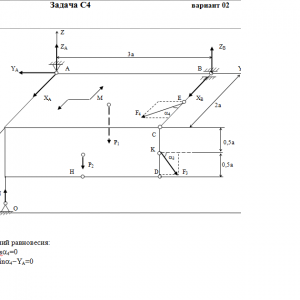
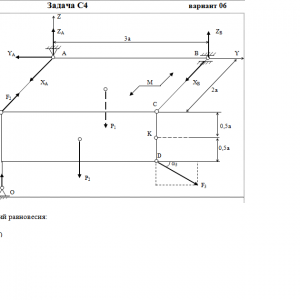
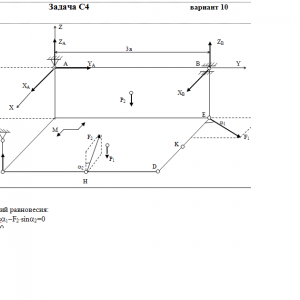
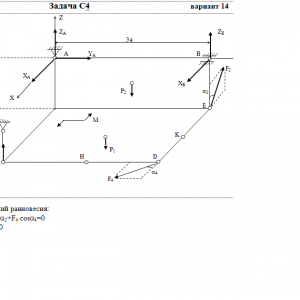
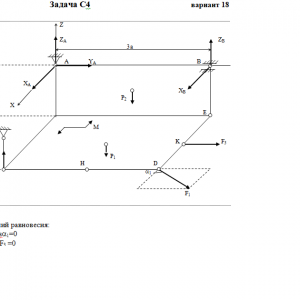
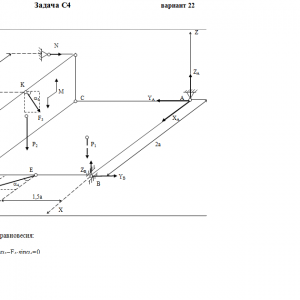
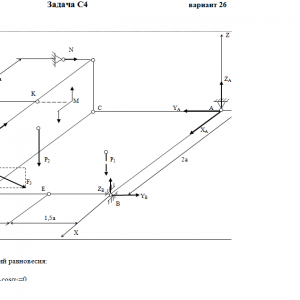
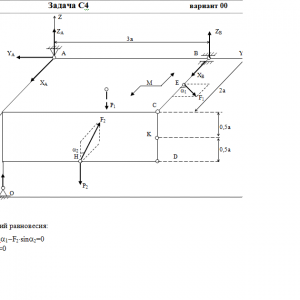
Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром (или подпятником)в точке A, цилиндрическим шарниром (подшипником) в точке В и невесомым стержнем 1 (рис. С4.0 — С4.7) или же двумя подшипниками в точках A и В и двумя невесомыми стержнями 1 и 2 (рис. С4.8, С4.9); все стержни прикреплены к плитам и к неподвижным опорам шарнирами.
Размеры плит указаны на рисунках; вес большей плиты Р1 = 5 кН, вес меньшей плиты Р2 = 3 кН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость xy — горизонтальная).
На плиты действуют пара сил с моментом М = 4 кН*м, лежащая в плоскости одной из плит, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С4; при этом силы F1 и F4 лежат в плоскостях, параллельных плоскости xy, сила F2 — в плоскости, параллельной xz, и сила F3 — в плоскости, параллельной yz. Точки приложения сил (D, E, H, K) находятся в углах или в серединах сторон плит.
Определить реакции связей в точках А и В и реакцию стержня (стержней). При подсчетах принять а = 0,6 м.Дано: P1=5 кН, P2=3 кН, M=4 кН*м, a=0,6 м, F1=6 кН, α1=60°, F2=8 кН, α2=30°
Найти: Найти реакции связейУказания. Задача С4 — на равновесие тела под действием произвольной пространственной системы сил. При ее решении учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) — две составляющие, лежащие в плоскости, перпендикулярной оси шарнира (подшипника). При вычислении момента силы F часто удобно разложить ее на две составляющие F‘ и F‘‘, параллельные координатным осям (или на три); тогда, по теореме Вариньона, mx(F) = mx((F‘) + mx(F‘‘) и т.д.
Тарг 1989 год задача С4 вариант 01
Описание
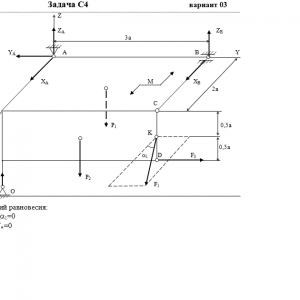
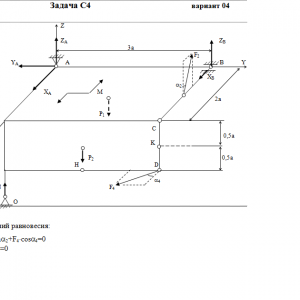
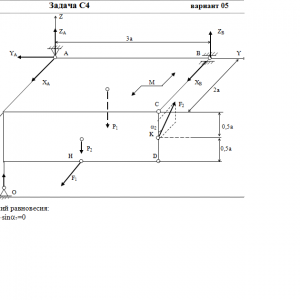
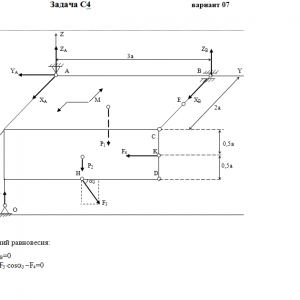
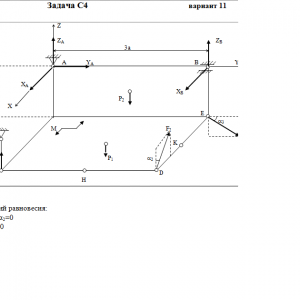
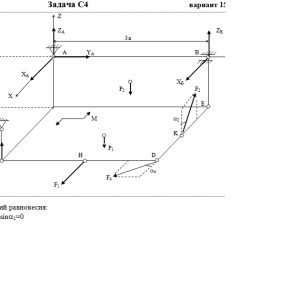
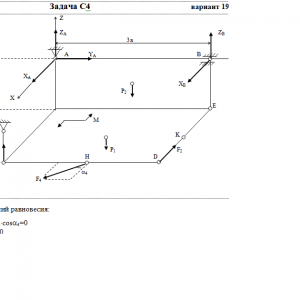
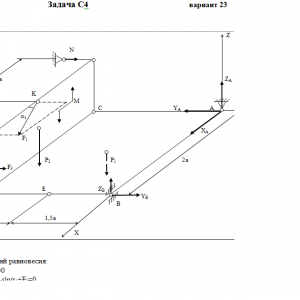
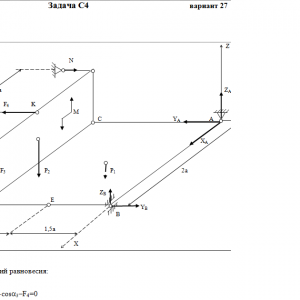
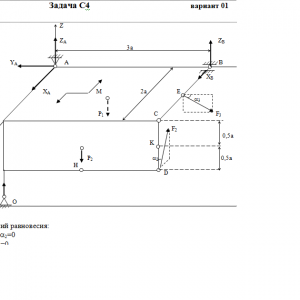
Две однородные прямоугольные тонкие плиты жестко соединены (сварены) под прямым углом друг к другу и закреплены сферическим шарниром (или подпятником)в точке A, цилиндрическим шарниром (подшипником) в точке В и невесомым стержнем 1 (рис. С4.0 — С4.7) или же двумя подшипниками в точках A и В и двумя невесомыми стержнями 1 и 2 (рис. С4.8, С4.9); все стержни прикреплены к плитам и к неподвижным опорам шарнирами.
Размеры плит указаны на рисунках; вес большей плиты Р1 = 5 кН, вес меньшей плиты Р2 = 3 кН. Каждая из плит расположена параллельно одной из координатных плоскостей (плоскость xy — горизонтальная).
На плиты действуют пара сил с моментом М = 4 кН*м, лежащая в плоскости одной из плит, и две силы. Значения этих сил, их направления и точки приложения указаны в табл. С4; при этом силы F1 и F4 лежат в плоскостях, параллельных плоскости xy, сила F2 — в плоскости, параллельной xz, и сила F3 — в плоскости, параллельной yz. Точки приложения сил (D, E, H, K) находятся в углах или в серединах сторон плит.
Определить реакции связей в точках А и В и реакцию стержня (стержней). При подсчетах принять а = 0,6 м.
Дано: P1=5 кН, P2=3 кН, M=4 кН*м, a=0,6 м, F2=8 кН, α2=60°, F3=10 кН, α3=30°
Найти: Найти реакции связей
Указания. Задача С4 — на равновесие тела под действием произвольной пространственной системы сил. При ее решении учесть, что реакция сферического шарнира (подпятника) имеет три составляющие (по всем трем координатным осям), а реакция цилиндрического шарнира (подшипника) — две составляющие, лежащие в плоскости, перпендикулярной оси шарнира (подшипника). При вычислении момента силы F часто удобно разложить ее на две составляющие F‘ и F‘‘, параллельные координатным осям (или на три); тогда, по теореме Вариньона, mx(F) = mx((F‘) + mx(F‘‘) и т.д.