Математика КрНУ Остроградского семестр 2
Методичка в формате pdf — ЗДЕСЬ
Вы можете выбрать один из вариантов заказать решение через форму. В случае если ваше задание отсутствует, перейдите в раздел Заказать новую работу и заполните необходимые поля.
Вы также можете связаться одним из указанных способов.
Вайбер
Вконтакте
Почта
Возможно решение задач онлайн (необходима предварительная связь).
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
Проверить, удовлетворяет ли указанному уравнению данная функция u.
Задание №4.
Исследовать на экстремум функцию.
Задание №5.
Найти наибольшее и наименьшее значения функции z=z(x,y) в области D−, ограниченной заданными линиями.
Задание №6.
Найти неопределенные интегралы.
Задание №7.
Вычислить определенные интегралы с точностью до двух знаков после запятой.
Задание №8.
Вычислить несобственные интегралы.
Задание №9
Вычислить площадь фигуры, ограниченной указанными линиями.
Задание №10.
Вычислить объем тела, полученного вращением фигуры Ф вокруг указанной оси координат.
Задание №11.
Вычислить длину дуги данной линии.
Задание №12.
Вычислить площадь поверхности, образованной вращением дуги кривой Lвокруг указанной оси.
Задание №13.
Найти координаты центра масс однородной плоской кривой L.
Задание №14.
Вычислить двойные и тройные интегралы.
Задание №15.
Вычислить площадь плоской области D, ограниченной заданными линиями.
Задание №16.
С помощью а) двойного и б) тройного интеграла вычислить объемы тел, ограниченных указанными поверхностями.
Задание №17.
Вычислить: а) массу неоднородной пластины D с поверхностной плотностью μ(х,у); б) статические моменты однородной пластины D относительно координатных осей, ограниченной заданными линиями.
Задание №18.
Вычислить: а) координаты центра масс; б) моменты инерции относительно координатных осей однородных тел V, ограниченных данными поверхностями.
Задание №19.
Вычислить данные криволинейные интегралы.
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
Представлено 30 товаров
-

Математика КрНУ, семестр 2 вариант 1, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2 вариант 10, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2 вариант 11, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2 вариант 2, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
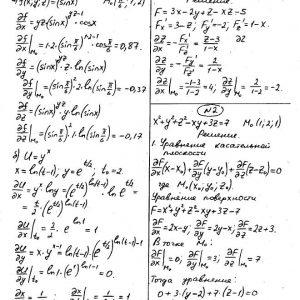
Математика КрНУ, семестр 2 вариант 3, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2 вариант 4, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
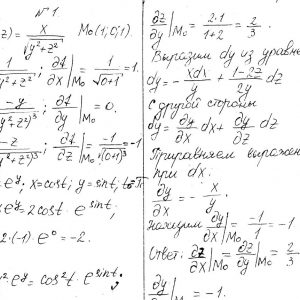
Математика КрНУ, семестр 2 вариант 5, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
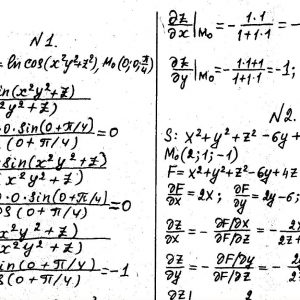
Математика КрНУ, семестр 2 вариант 6, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
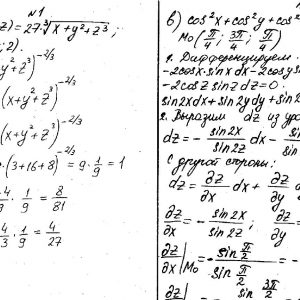
Математика КрНУ, семестр 2 вариант 7, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2 вариант 8, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
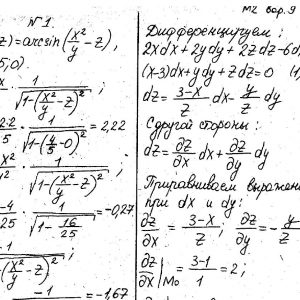
Математика КрНУ, семестр 2 вариант 9, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
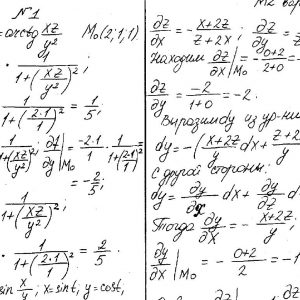
Математика КрНУ, семестр 2, вариант 12, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
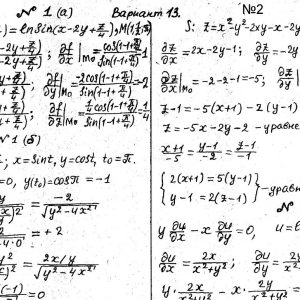
Математика КрНУ, семестр 2, вариант 13, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 14, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 15, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
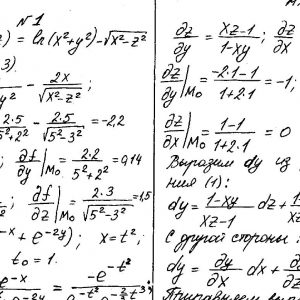
Математика КрНУ, семестр 2, вариант 16, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
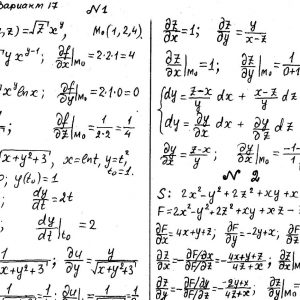
Математика КрНУ, семестр 2, вариант 17, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 18, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 19, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
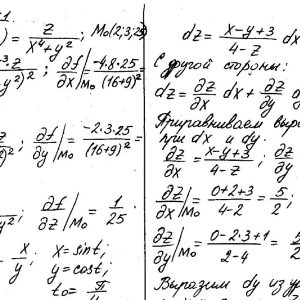
Математика КрНУ, семестр 2, вариант 20, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 21, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
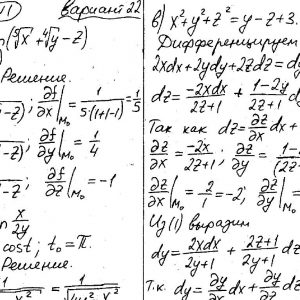
Математика КрНУ, семестр 2, вариант 22, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
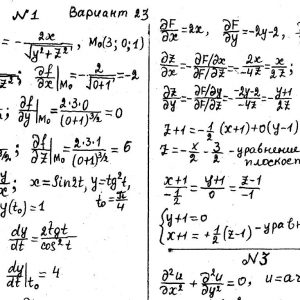
Математика КрНУ, семестр 2, вариант 23, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
Математика КрНУ, семестр 2, вариант 24, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
Математика КрНУ, семестр 2, вариант 25, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 26, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
Математика КрНУ, семестр 2, вариант 27, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
Математика КрНУ, семестр 2, вариант 28, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
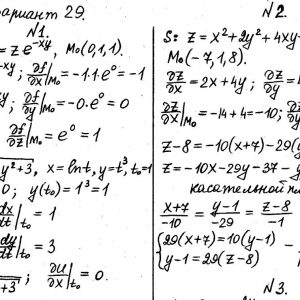
Математика КрНУ, семестр 2, вариант 29, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 30, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину