Математика
Отображение 97–128 из 177
-
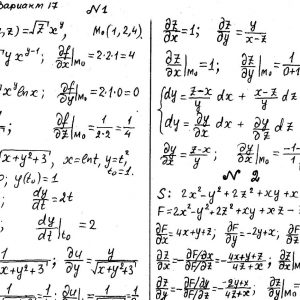
Математика КрНУ, семестр 2, вариант 17, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 18, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 19, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
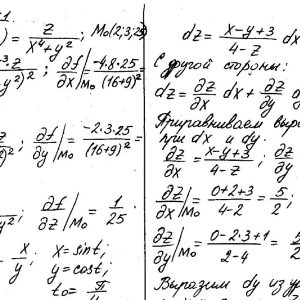
Математика КрНУ, семестр 2, вариант 20, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 21, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
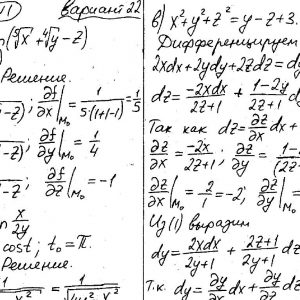
Математика КрНУ, семестр 2, вариант 22, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
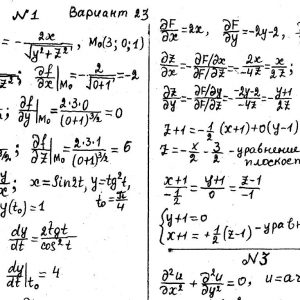
Математика КрНУ, семестр 2, вариант 23, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
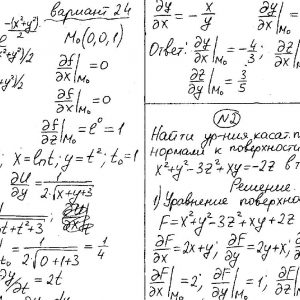
Математика КрНУ, семестр 2, вариант 24, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
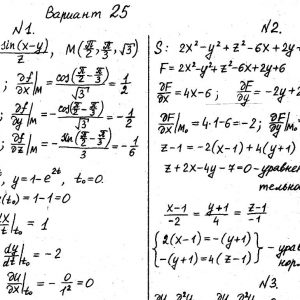
Математика КрНУ, семестр 2, вариант 25, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 26, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
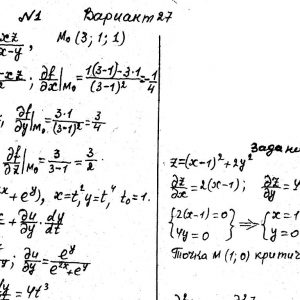
Математика КрНУ, семестр 2, вариант 27, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
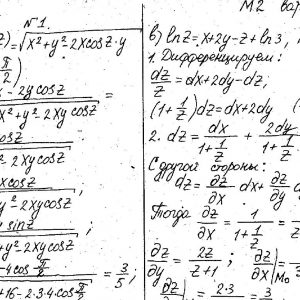
Математика КрНУ, семестр 2, вариант 28, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -
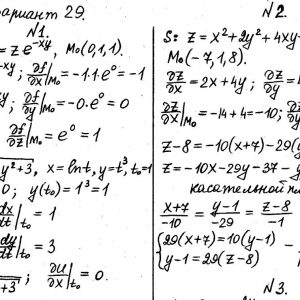
Математика КрНУ, семестр 2, вариант 29, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 2, вариант 30, семестровая №1-20
Описание
Кременчугский национальный университет имени Михаила Остроградского, Функции нескольких переменных, интегральное исчисление. Задания 1-20.
Задание №1.
Вычислить значения частных производных.
Задание №2.
Найти уравнения касательной и нормали к заданной поверхности в точке М0(х0, у0, z0).
Задание №3.
…
Задание №20.
Доказать, что данной выражение является полным дифференциалом функции u(x,y). Найти функцию u(x,y).
В галерее для примера находится номер 16 варианта 1.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 1, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 10, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 11, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 12, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 13, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 14, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
Методичка с заданием доступна по ссылке:
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 15, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 16, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 17, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
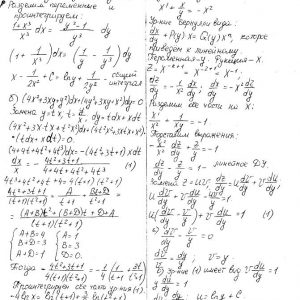
Математика КрНУ, семестр 3, вариант 18, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 19, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 2, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
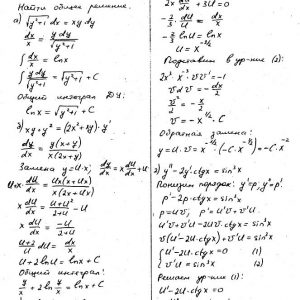
Математика КрНУ, семестр 3, вариант 20, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 21, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
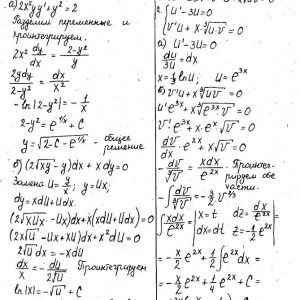
Математика КрНУ, семестр 3, вариант 22, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
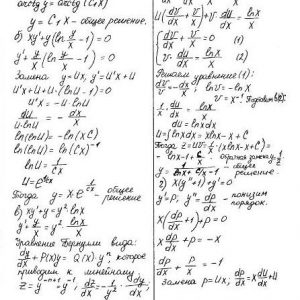
Математика КрНУ, семестр 3, вариант 23, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -
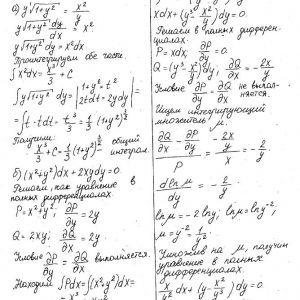
Математика КрНУ, семестр 3, вариант 24, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину -

Математика КрНУ, семестр 3, вариант 25, семестровая N 1-13
Описание
Кременчугский национальный университет имени Михаила Остроградского, Обыкновенные дифференциальные уравнения и ряды. Задания 1-13.
Задание 1. Найти общее решение (общий интеграл) дифференциального уравнения.
Задание 2. Найти частное решение дифференциального уравнения, удовлетворяющее данным начальным условиям.
Задание 3. Решить дифференциальное уравнение методом вариации произвольных постоянных.
……….
Задание 13. Разложить в ряд Фурье в указанном интервале периодическую функцию f(x) с периодом ω=2ℓ.
2.00 $ В корзину