Теоретическая механика методичка Тарга 1989
Отображение 257–288 из 1113
-

Тарг 1989 год задача Д11 вариант 69
Описание
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=2P, P2=P3=0, P4=P, P5=0, F=0, M1=2PR, M2=0, пружина AB
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 70
Описание
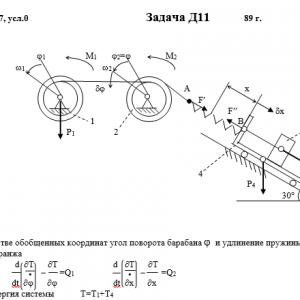
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=4P, P2=0, P3=P5=0, P4=3P, F=4P, M1=0, M2=0, пружина AB
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 71
Описание
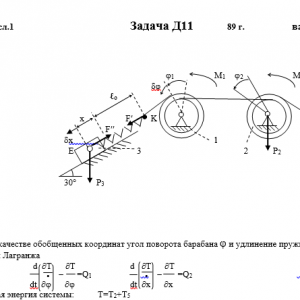
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=0, P2=2P, P3=P4=0, P5=3P, F=0, M1=0, M2=-2PR, пружина KE
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -

Тарг 1989 год задача Д11 вариант 72
Описание
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=0, P2=2P, P3=P5=0, P4=P, F=0, M1=2PR, M2=0, пружина AB
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 73
Описание
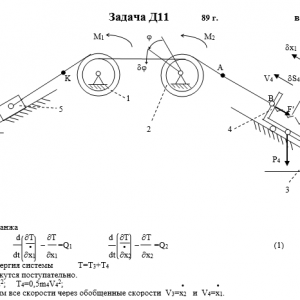
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=P2=0, P3=2P, P4=5P, P5=0, F=0, M1=0, M2=2PR, пружина BD
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -

Тарг 1989 год задача Д11 вариант 75
Описание
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=P2=0, P3=4P, P4=3P, P5=0, F=P, M1=0, M2=0, пружина BD
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 76
Описание
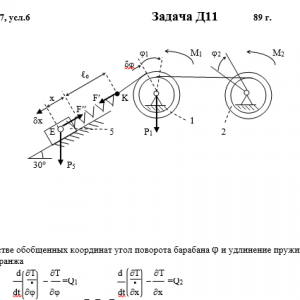
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=2P, P2=0, P3=P4=0, P5=P, F=0, M1=0, M2=-PR, пружина KE
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 78
Описание
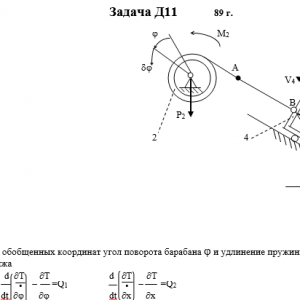
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=0, P2=4P, P3=2P, P4=P5=0, F=0, M1=0, M2=3PR, пружина BD
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 79
Описание
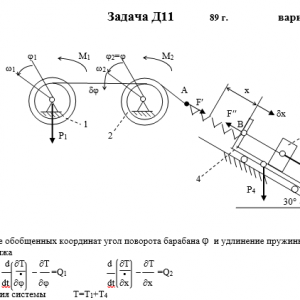
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=2P, P2=0, P3=P5=0, P4=P, F=0, M1=2PR, M2=0, пружина AB
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -

Тарг 1989 год задача Д11 вариант 84
Описание
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=P, P2=0, P3=P4=0, P5=4P, F=0, M1=-PR, M2=0, пружина KE
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 85
Описание
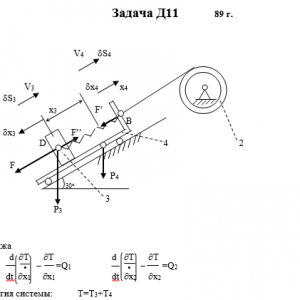
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=P2=0, P3=4P, P4=3P, P5=P, F=P, M1=0, M2=0, пружина BD
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 86
Описание
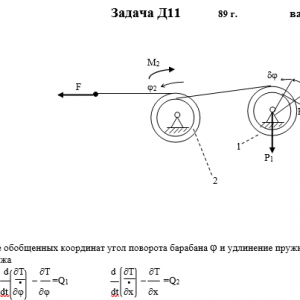
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=2P, P2=0, P3=P4=0, P5=P, F=0, M1=0, M2=-PR, пружина KE
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 88
Описание
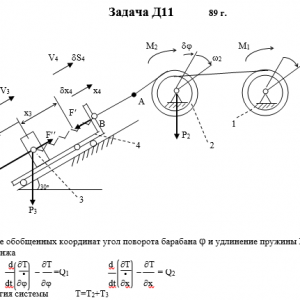
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=0, P2=2P, P3=2P, P4=P5=0, F=0, M1=0, M2=3PR, пружина BD
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 90
Описание
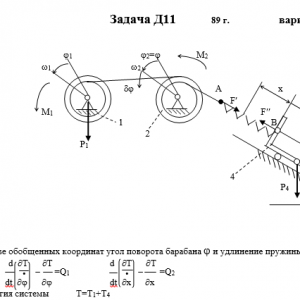
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=4P, P2=0, P3=P5=0, P4=3P, F=3P, M1=0, M2=0, пружина AB
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -

Тарг 1989 год задача Д11 вариант 91
Описание
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=0, P2=2P, P3=P4=0, P5=3P, F=0, M1=0, M2=-PR, пружина KE
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 92
Описание
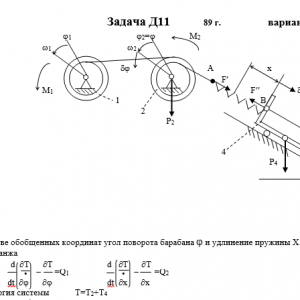
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=0, P2=2P, P3=P5=0, P4=P, F=0, M1=2PR, M2=0, пружина AB
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 93
Описание
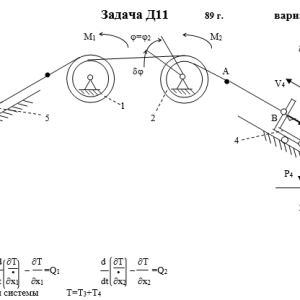
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=P2=0, P3=2P, P4=5P, P5=0, F=0, M1=0, M2=2PR, пружина BD
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -

Тарг 1989 год задача Д11 вариант 94
Описание
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=P, P2=P3=P4=0, P5=4P, F=0, M1=-PR, M2=0, пружина KE
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 96
Описание
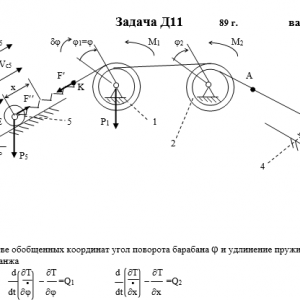
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=2P, P2=P3=P4=0, P5=P, F=0, M1=0, M2=-PR, пружина KE
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 97
Описание
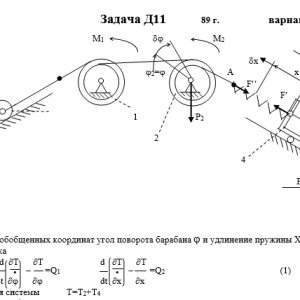
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=0, P2=4P, P3=P5=0, P4=2P, F=3P, M1=0, M2=2PR, пружина AB
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -
Тарг 1989 год задача Д11 вариант 98
Описание
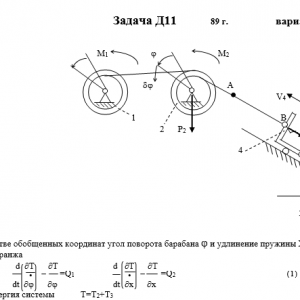
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=0, P2=4P, P3=2P, P4=P5=0, F=0, M1=0, M2=3PR, пружина AB
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -

Тарг 1989 год задача Д11 вариант 99
Описание
Механическая система состоит из тел 1, 2,…5 весом P1, Р2,…,P5 соответственно, связанных друг с другом нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д11.0 — Д11.9, табл. Д11). Радиусы ступенчатых блоков 1 и 2 равны соответственно R1=R, r1=0,4R, R2=R, r2=0,8R. При вычислении моментов инерции все блоки, катки и колеса считать однородными сплошными цилиндрами радиуса R.
На систему кроме сил тяжести действует сила F, приложенная к телу 3 или 4 (если тело 3 в систему не входит, сила приложена в точке В к тележке), и пары сил с моментами М1, М2, приложенные к блокам 1 и 2; когда М<0, направление момента противоположно показанному на рисунке.
На участке нити, указанном в таблице в столбце «Пружина», включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если AD, то AD — пружина и т.д.); в начальный момент времени пружина не деформирована.
Составить для системы уравнения Лагранжа и найти закон изменения обобщенной координаты х, т. е. х = f(t), считая, что движение начинается из состояния покоя; определить также частоту и период колебаний, совершаемых телами системы при ее движении (о выборе координаты х см. Указания).
Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит; дли колес, обозначенных номером 4, P4 — их общий вес (вес платформы такой тележки не учитывается).Дано: R1=R, r1=0,4R, R2=R, r2=0,8R, P1=2P, P2=P3=0, P4=P, P5=0, F=0, M1=2PR, M2=0, пружина AB
1.00 $ В корзину
Составить уравнения Лагранжа, найти: k, τ -

Тарг 1989 год задача Д12 вариант 33
Описание
Механизм, расположенный в вертикальной плоскости (рис. Д12.0-Д12.9), состоит из ступенчатых колес 1 и 2 с радиусами R1=0,4 м, r1=0,2 м, R2=0,5 м, r2=0,3 м, имеющих неподвижные оси вращения однородного стержня 3 длиной l=1,2 м, закрепленного шарниром на одном из концов; грузов 4 и 5, подвешенных к нитям, намотанным на колеса. На стержне расстояние АВ = 2l/3.
Стержень 3 соединен с колесом 2 невесомым стержнем 6. Колеса 1 и 2 или находятся в зацеплении (рис. 0—4), или соединены невесомым стержнем 7 (рис. 5-9). К колесам и стержню 3 прикреплены пружины.
В табл. Д 12 заданы массы mi, тел (кг) и коэффициенты жесткости Ci пружин (Н/м). Прочерки в столбцах таблицы означают, что соответствующие тела или пружины в систему не входят (на чертеже эти тела и пружины не изображать); в результате в каждом конкретном варианте получается довольно простой механизм, содержащий три или даже два тела. Стержень 6 или 7 входит в состав механизма, когда в него входят оба тела, соединенные этим стержнем.
В положениях, изображенных на рисунках, механизм находится в равновесии. Определить частоту и период малых колебаний системы около положения равновесия. Найти также, чему равно статическое удлинение (сжатие) пружины λст в положении равновесия.
При подсчетах считать колеса 1 и 2 сплошными однородными цилиндрами радиусов R1 и R2 соответственно.Дано: m1=20 кг, m2=6 кг, C1=1500 Н/м, R1=0,4 м, r1=0,2 м,
1.00 $ В корзину
Найти: К, τ, λст -
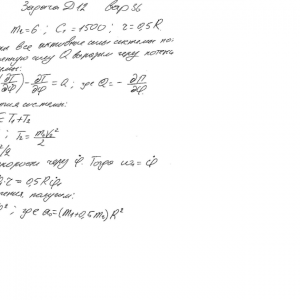
Тарг 1989 год задача Д12 вариант 63
Описание
Механизм, расположенный в вертикальной плоскости (рис. Д12.0-Д12.9), состоит из ступенчатых колес 1 и 2 с радиусами R1=0,4 м, r1=0,2 м, R2=0,5 м, r2=0,3 м, имеющих неподвижные оси вращения однородного стержня 3 длиной l=1,2 м, закрепленного шарниром на одном из концов; грузов 4 и 5, подвешенных к нитям, намотанным на колеса. На стержне расстояние АВ = 2l/3.
Стержень 3 соединен с колесом 2 невесомым стержнем 6. Колеса 1 и 2 или находятся в зацеплении (рис. 0—4), или соединены невесомым стержнем 7 (рис. 5-9). К колесам и стержню 3 прикреплены пружины.
В табл. Д 12 заданы массы mi, тел (кг) и коэффициенты жесткости Ci пружин (Н/м). Прочерки в столбцах таблицы означают, что соответствующие тела или пружины в систему не входят (на чертеже эти тела и пружины не изображать); в результате в каждом конкретном варианте получается довольно простой механизм, содержащий три или даже два тела. Стержень 6 или 7 входит в состав механизма, когда в него входят оба тела, соединенные этим стержнем.
В положениях, изображенных на рисунках, механизм находится в равновесии. Определить частоту и период малых колебаний системы около положения равновесия. Найти также, чему равно статическое удлинение (сжатие) пружины λст в положении равновесия.
При подсчетах считать колеса 1 и 2 сплошными однородными цилиндрами радиусов R1 и R2 соответственно.Дано: m1=20 кг, m2=6 кг, C1=1500 Н/м, r=0,5R
1.00 $ В корзину
Найти: К, τ, λст -

Тарг 1989 год задача Д12 вариант 66
Описание
Механизм, расположенный в вертикальной плоскости (рис. Д12.0-Д12.9), состоит из ступенчатых колес 1 и 2 с радиусами R1=0,4 м, r1=0,2 м, R2=0,5 м, r2=0,3 м, имеющих неподвижные оси вращения однородного стержня 3 длиной l=1,2 м, закрепленного шарниром на одном из концов; грузов 4 и 5, подвешенных к нитям, намотанным на колеса. На стержне расстояние АВ = 2l/3.
Стержень 3 соединен с колесом 2 невесомым стержнем 6. Колеса 1 и 2 или находятся в зацеплении (рис. 0—4), или соединены невесомым стержнем 7 (рис. 5-9). К колесам и стержню 3 прикреплены пружины.
В табл. Д 12 заданы массы mi, тел (кг) и коэффициенты жесткости Ci пружин (Н/м). Прочерки в столбцах таблицы означают, что соответствующие тела или пружины в систему не входят (на чертеже эти тела и пружины не изображать); в результате в каждом конкретном варианте получается довольно простой механизм, содержащий три или даже два тела. Стержень 6 или 7 входит в состав механизма, когда в него входят оба тела, соединенные этим стержнем.
В положениях, изображенных на рисунках, механизм находится в равновесии. Определить частоту и период малых колебаний системы около положения равновесия. Найти также, чему равно статическое удлинение (сжатие) пружины λст в положении равновесия.
При подсчетах считать колеса 1 и 2 сплошными однородными цилиндрами радиусов R1 и R2 соответственно.Дано: m1=12 кг, m3=8 кг, m4=4 кг, C3=1200 Н/м
1.00 $ В корзину
Найти: К, τ, λст -
Тарг 1989 год задача Д2 вариант 00
Описание
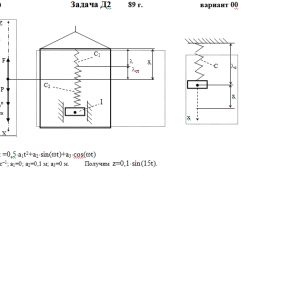
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a1t2+a2*sin(ωt)+a3*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3 — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v0— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с1, с2, с3 означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=1 кг, с1=300 Н/м, с2=150 Н/м, a1=0 м/с2, a2=0,1 м, a3=0 м, ω=15 с-1, μ=0 Н*с/м, λ0=0 м, V0=0 м/с
1.00 $ В корзину
Найти: x(t) -

Тарг 1989 год задача Д2 вариант 01
Описание
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a1t2+a2*sin(ωt)+a3*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3 — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v0— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с1, с2, с3 означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=0,8 кг, с1=300 Н/м, с2=150 Н/м, a1=0 м/с2, a2=0,1 м, a3=0 м, ω=15 с-1, μ=0 Н*с/м, λ0=0 м, V0=0 м/с
1.00 $ В корзину
Найти: x(t) -
Тарг 1989 год задача Д2 вариант 02
Описание
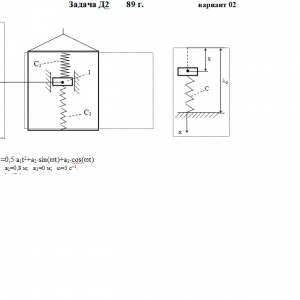
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a1t2+a2*sin(ωt)+a3*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3 — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v0— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с1, с2, с3 означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=0,5 кг, с1=100 Н/м, с3=150 Н/м, a1=0 м/с2, a2=0,8 м, a3=0 м, ω=5 с-1, λ0=0 м, V0=4 м/с
1.00 $ В корзину
Найти: x(t) -

Тарг 1989 год задача Д2 вариант 03
Описание
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a1t2+a2*sin(ωt)+a3*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3 — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v0— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с1, с2, с3 означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=1 кг, с1=240 Н/м, с3=160 Н/м, a1=0 м/с2, a2=0 м, a3=0,5 м, ω=6 с-1, μ= 0 Н*с/м λ0=0 м, V0=0 м/с
1.00 $ В корзину
Найти: x(t) -
Тарг 1989 год задача Д2 вариант 05
Описание
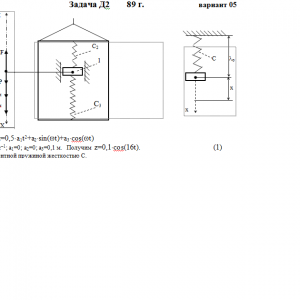
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a1t2+a2*sin(ωt)+a3*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3 — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v0— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с1, с2, с3 означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=2 кг, с2=400 Н/м, с3=400 Н/м, a1=0 м/с2, a2=0 м, a3=0,1 м, ω=16 с-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
1.00 $ В корзину
Найти: x(t) -
Тарг 1989 год задача Д2 вариант 06
Описание
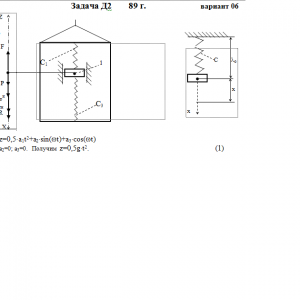
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a1t2+a2*sin(ωt)+a3*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3 — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v0— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с1, с2, с3 означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=0,4 кг, с1=60 Н/м, с3=180 Н/м, a1=g м/с2, a2=0 м, a3=0 м, μ= 4 Н*с/м, λ0=0 м, V0=2 м/с
1.00 $ В корзину
Найти: x(t) -
Тарг 1989 год задача Д2 вариант 07
Описание
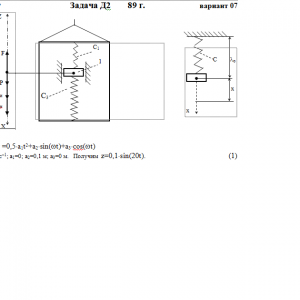
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону z =0,5*a1t2+a2*sin(ωt)+a3*cos(ωt) (ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R = μv, где v — скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т. е. х = f(t); начало координат поместить в точке, где находится прикрепленный к грузу конец пружины, когда пружина не деформирована. При этом во избежание ошибок в знаках направить ось х в сторону удлинения пружины, а груз изобразить в положении, при котором х> 0, т. е. пружина растянута. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3 — коэффициенты жесткости пружин, λо — удлинение пружины с эквивалентной жесткостью в начальный момент времени t = 0, v0— начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк в столбцах с1, с2, с3 означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин.
Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=0,5 кг, с1=120 Н/м, с3=180 Н/м, a1=0 м/с2, a2=0,1 м, a3=0 м, ω=20 с-1, μ= 0 Н*с/м, λ0=0 м, V0=0 м/с
1.00 $ В корзину
Найти: x(t)