Описание
Задачи по дискретной математике и комбинаторике.
Решены первые 4 задачи из методички, а также задачи 6 и 8
метод дискретная
Завдання №1
Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.
Завдання №2
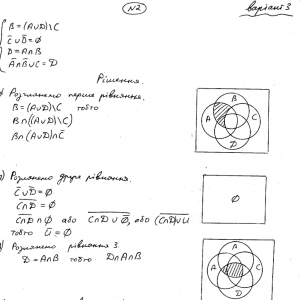
Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.
Завдання №3
Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).
Завдання №4
Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
Необхідно :
– зобразити граф графічно й у вигляді матриці інциденцій;
– визначити хроматичне число графа;
– використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.
Завдання №6
Транспортна мережа задана за допомогою таблиці, де зазначені дуги мережі та пропускну спроможність цих дуг. Необхідно зобразити граф графічно і, використовуючи теорему Форда-Фалкерсона, визначити найбільший потік у мережі (s – джерело, t – стік).
Завдання № 8
1. Функцію f(x1, x2, x3,x4) записати у вигляді таблиці істинності та у вигляді нормальної та досконалої формах зображення.
2. Методом резолюцій довести, що одна з формул є логічним наслідком деяких висловів або впевнитись у противному.