Магазин
Отображение 1985–2016 из 3934
-
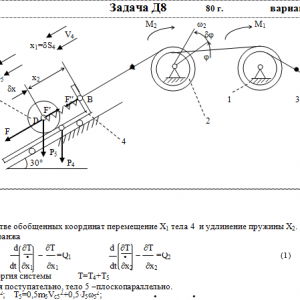
Тарг 1980 год задача Д8 вариант 73
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=P3=0, P4=3P, P5=2P, F=P, M1=0, M2=0, пружина BD Найти: Составить уравнения Лагранжа, k-?, τ-? -
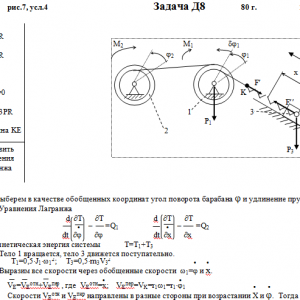
Тарг 1980 год задача Д8 вариант 74
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=2P, P4=P5=0, F=0, M1= -3PR, M2=0, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
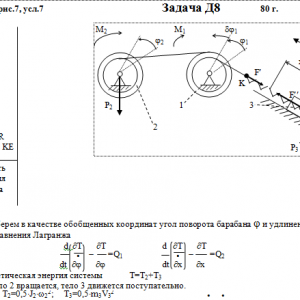
Тарг 1980 год задача Д8 вариант 77
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P, P4=P5=0, F=0, M1=0, M2= -2PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
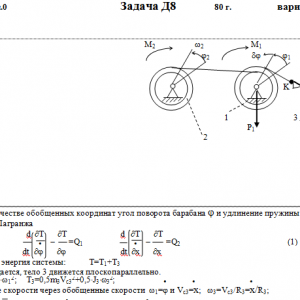
Тарг 1980 год задача Д8 вариант 80
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=P, P4=P5=0, F=0, M1=0, M2= -3PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 81
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
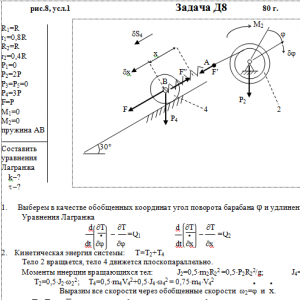
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P5=0, P4=3P, F=P, M1=0, M2=0, пружина AB Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 82
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
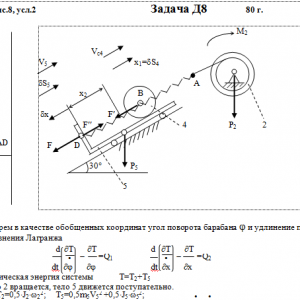
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=P, P3=P4=0, P5=2P, F=0, M1=2PR, M2=0, пружина AD Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 87
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
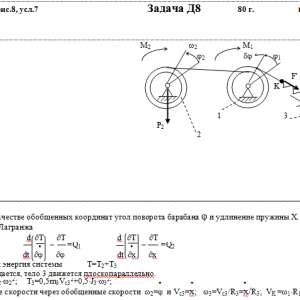
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P, P4=P5=0, F=0, M1=0, M2= -2*PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 89
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
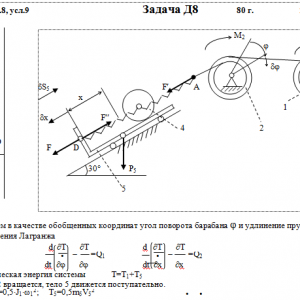
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=2P, P2=0, P3=P4=0, P5=P, F=3P, M1=0, M2=0, пружина AD Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 90
Описание
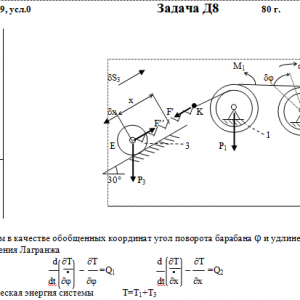
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=P, F=0, M1=0, M2= -3PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 94
Описание
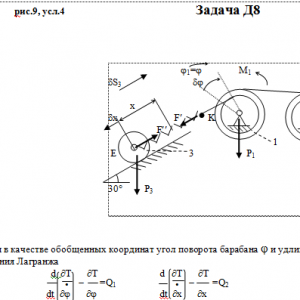
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P2=P4=P5=0, P1=P, P3=2P, F=0, M1= -3PR, M2=0, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 95
Описание
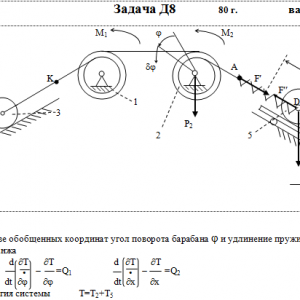
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P4=0, P5=P, F=0, M1=0, M2=4PR, пружина AD Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 97
Описание
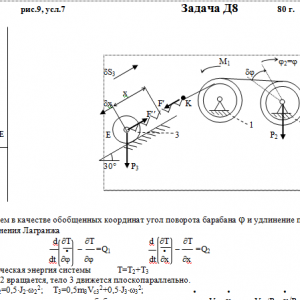
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P4=P5=0, P2=2P, P3=P, F=0, M1=0, M2= -2PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д9 вариант 44
Описание
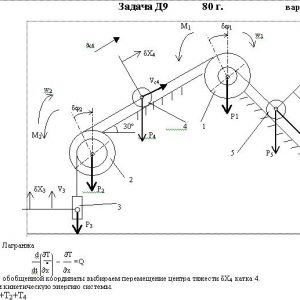
Механическая система состоит из ступенчатых шкивов 1 и 2 весом Р1 и Р2 с радиусами ступеней R1 = R, r1 = 0,4R, R2 = R, r2 = 0,8R (массу каждого шкива считать равномерно распределенной по его внешнему ободу) и грузов или сплошных однородных цилиндрических катков 3, 4, 5 весом Р3, P4, Р5 соответственно (рис. Д9.0 —Д9.9, табл. Д9). Тела системы соединены нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Грузы скользят по плоскостям без трения, а катки катятся без скольжения.
Кроме сил тяжести на одно из тел системы действует постоянная сила F, а на шкивы 1 и 2 при их вращении действуют постоянные моменты сил сопротивления, равные соответственно М1 и М2.
Составить для данной системы уравнение Лагранжа и определить из него величину, указанную в таблице в столбце Найти, где обозначено: ε1, ε2 — угловые ускорения шкивов 1 и 2, аC3, аC4, аC5 — ускорения центров масс тел 3, 4, 5 (если тело 3 или 4 — груз, то аСз = а3, аС4 = а4, где а3 и а4 — ускорения соответствующих грузов). Когда в задаче надо определить ε1 или ε2, считать R = 0,25 м.
То из тел 3, 4, вес которого равен нулю, на чертеже не изображать. Шкивы 1 и 2 всегда входят в систему.Дано: P1=8P, P2=6P, P3=0, P4=3P, P5=0, М1=0,4PR, M2=0,3PR, F=8P, R1=R, r1=0,4R, R2=R, r2=0,8R
1.00 $ В корзину
Найти: aC4 -
Тарг 1980 год задача Д9 вариант 62
Описание
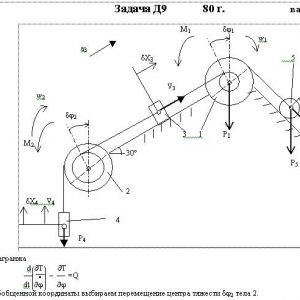
Механическая система состоит из ступенчатых шкивов 1 и 2 весом Р1 и Р2 с радиусами ступеней R1 = R, r1 = 0,4R, R2 = R, r2 = 0,8R (массу каждого шкива считать равномерно распределенной по его внешнему ободу) и грузов или сплошных однородных цилиндрических катков 3, 4, 5 весом Р3, P4, Р5 соответственно (рис. Д9.0 —Д9.9, табл. Д9). Тела системы соединены нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Грузы скользят по плоскостям без трения, а катки катятся без скольжения.
Кроме сил тяжести на одно из тел системы действует постоянная сила F, а на шкивы 1 и 2 при их вращении действуют постоянные моменты сил сопротивления, равные соответственно М1 и М2.
Составить для данной системы уравнение Лагранжа и определить из него величину, указанную в таблице в столбце Найти, где обозначено: ε1, ε2 — угловые ускорения шкивов 1 и 2, аC3, аC4, аC5 — ускорения центров масс тел 3, 4, 5 (если тело 3 или 4 — груз, то аСз = а3, аС4 = а4, где а3 и а4 — ускорения соответствующих грузов). Когда в задаче надо определить ε1 или ε2, считать R = 0,25 м.
То из тел 3, 4, вес которого равен нулю, на чертеже не изображать. Шкивы 1 и 2 всегда входят в систему.Дано: P1=8Р, P2=0, P3=0, P4=2Р, P5=P, М1=0,3PR, M2=0, F=6P, R1=R, r1=0,4R, R2=R, r2=0,8R
1.00 $ В корзину
Найти: ε2 -
Тарг 1980 год задача Д9 вариант 69
Описание
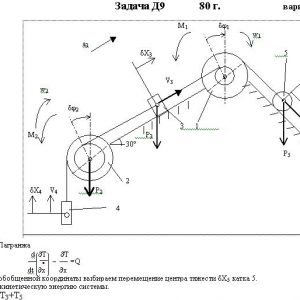
Механическая система состоит из ступенчатых шкивов 1 и 2 весом Р1 и Р2 с радиусами ступеней R1 = R, r1 = 0,4R, R2 = R, r2 = 0,8R (массу каждого шкива считать равномерно распределенной по его внешнему ободу) и грузов или сплошных однородных цилиндрических катков 3, 4, 5 весом Р3, P4, Р5 соответственно (рис. Д9.0 —Д9.9, табл. Д9). Тела системы соединены нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Грузы скользят по плоскостям без трения, а катки катятся без скольжения.
Кроме сил тяжести на одно из тел системы действует постоянная сила F, а на шкивы 1 и 2 при их вращении действуют постоянные моменты сил сопротивления, равные соответственно М1 и М2.
Составить для данной системы уравнение Лагранжа и определить из него величину, указанную в таблице в столбце Найти, где обозначено: ε1, ε2 — угловые ускорения шкивов 1 и 2, аC3, аC4, аC5 — ускорения центров масс тел 3, 4, 5 (если тело 3 или 4 — груз, то аСз = а3, аС4 = а4, где а3 и а4 — ускорения соответствующих грузов). Когда в задаче надо определить ε1 или ε2, считать R = 0,25 м.
То из тел 3, 4, вес которого равен нулю, на чертеже не изображать. Шкивы 1 и 2 всегда входят в систему.Дано: P1=0, P2=6P, P3=5P, P4=0, P5=6P, М1=0,2PR, M2=0, F=10P, R1=R, r1=0,4R, R2=R, r2=0,8R
1.00 $ В корзину
Найти: aC5 -
Тарг 1980 год задача Д9 вариант 70
Описание
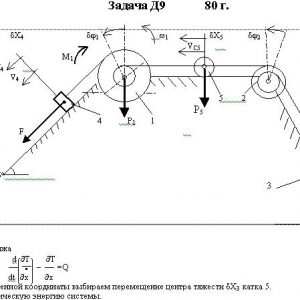
Механическая система состоит из ступенчатых шкивов 1 и 2 весом Р1 и Р2 с радиусами ступеней R1 = R, r1 = 0,4R, R2 = R, r2 = 0,8R (массу каждого шкива считать равномерно распределенной по его внешнему ободу) и грузов или сплошных однородных цилиндрических катков 3, 4, 5 весом Р3, P4, Р5 соответственно (рис. Д9.0 —Д9.9, табл. Д9). Тела системы соединены нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям. Грузы скользят по плоскостям без трения, а катки катятся без скольжения.
Кроме сил тяжести на одно из тел системы действует постоянная сила F, а на шкивы 1 и 2 при их вращении действуют постоянные моменты сил сопротивления, равные соответственно М1 и М2.
Составить для данной системы уравнение Лагранжа и определить из него величину, указанную в таблице в столбце Найти, где обозначено: ε1, ε2 — угловые ускорения шкивов 1 и 2, аC3, аC4, аC5 — ускорения центров масс тел 3, 4, 5 (если тело 3 или 4 — груз, то аСз = а3, аС4 = а4, где а3 и а4 — ускорения соответствующих грузов). Когда в задаче надо определить ε1 или ε2, считать R = 0,25 м.
То из тел 3, 4, вес которого равен нулю, на чертеже не изображать. Шкивы 1 и 2 всегда входят в систему.Дано: P1=10Р, P2=0, P3=4Р, P4=0, P5=3P, М1=0,2PR, M2=0, F=10P, R1=R, r1=0,4R, R2=R, r2=0,8R
1.00 $ В корзину
Найти: аС3 -
Тарг 1980 год задача К1 вариант 23
Описание
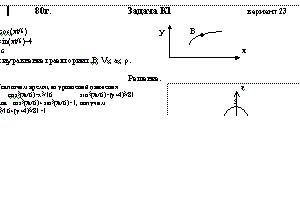
Точка В движется в плоскости ху (рис. К1.0—К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями х = f1(t), y=f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х = f1(t) указана непосредственно на рисунках, а зависимость у = f2(t) дана в табл. К1 (для рис. О — 2 в столбце 2, для рис. 3 — 6 в столбце 3, для рис. 7 — 9 в столбце 4). Как и в задачах С1—С5, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 — по последней.Дано: х=4*cos(πt/6), y=9*sin(πt/6)-4, t=1 c
1.00 $ В корзину
Найти: уравнение траектории т.В; VB; aB; ρ. -
Тарг 1980 год задача К1 вариант 46
Описание
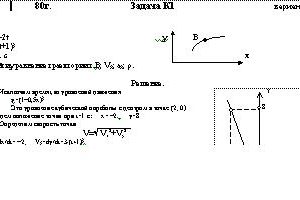
Точка В движется в плоскости ху (рис. К1.0—К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями х = f1(t), y=f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х = f1(t) указана непосредственно на рисунках, а зависимость у = f2(t) дана в табл. К1 (для рис. О — 2 в столбце 2, для рис. 3 — 6 в столбце 3, для рис. 7 — 9 в столбце 4). Как и в задачах С1—С5, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 — по последней.Дано: х=-2t, y=(t+1)3, t=1 c
1.00 $ В корзину
Найти: уравнение траектории т.В; VB; aB; ρ. -
Тарг 1980 год задача К1 вариант 55
Описание
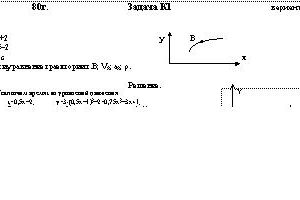
Точка В движется в плоскости ху (рис. К1.0—К1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями х = f1(t), y=f2(t), где х и у выражены в сантиметрах, t — в секундах.
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость х = f1(t) указана непосредственно на рисунках, а зависимость у = f2(t) дана в табл. К1 (для рис. О — 2 в столбце 2, для рис. 3 — 6 в столбце 3, для рис. 7 — 9 в столбце 4). Как и в задачах С1—С5, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 — по последней.Дано: х=2t+2, y=3t2-2, t=1 c
1.00 $ В корзину
Найти: уравнение траектории т.В; VB; aB; ρ. -
Тарг 1980 год задача К2 вариант 23
Описание
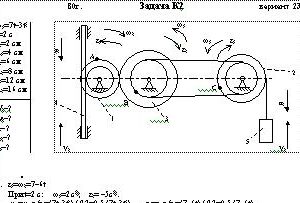
Плоский механизм состоит из стержней 1 — 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами (рис. К2.0 — К2.9). Длины стержней равны: l1= 0,4 м, l2 = 1,2 м, l3 = 1,4 м, l4 = 0,8 м.
Положение механизма определяется углами α, β, γ, φ, θ, которые вместе с другими величинами заданы в табл. К2. Точка D на всех рисунках и точка К на рис. 7 — 9 в середине соответствующего стержня. Определить величины, указанные в таблице в столбце „Найти».
Дуговые стрелки на рисунках показывают, как при построении чертежа должны откладываться соответствующие углы, т. е. по ходу или против хода часовой стрелки (например, угол γ на рис. 1 следует отложить от стержня DE против хода часовой стрелки, а на рис. 2 — oт стержня АЕ по ходу часовой стрелки).
Построение чертежа начинать со стержня, направление которого определяется углом α; ползун В и его направляющие для большей наглядности изобразить, как в примере К2 (см. рис. К2). Заданную угловую скорость считать направленной против хода часовой стрелки, а заданную скорость vB — oт точки В к Ь.Дано: ω2=7t-3t2, t=2 c, r1=2 см, R1=4 см, r2= 6 см, R2=8 см, r3=12 см, R3=16 см
1.00 $ В корзину
Найти: V5, ω3, ε2, aA, a4 -
Тарг 1980 год задача К2 вариант 46
Описание
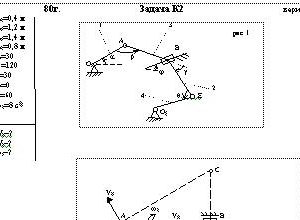
Плоский механизм состоит из стержней 1 — 4 и ползуна В, соединенных друг с другом и с неподвижными опорами О1 и О2 шарнирами (рис. К2.0 — К2.9). Длины стержней равны: l1= 0,4 м, l2 = 1,2 м, l3 = 1,4 м, l4 = 0,8 м.
Положение механизма определяется углами α, β, γ, φ, θ, которые вместе с другими величинами заданы в табл. К2. Точка D на всех рисунках и точка К на рис. 7 — 9 в середине соответствующего стержня. Определить величины, указанные в таблице в столбце „Найти».
Дуговые стрелки на рисунках показывают, как при построении чертежа должны откладываться соответствующие углы, т. е. по ходу или против хода часовой стрелки (например, угол γ на рис. 1 следует отложить от стержня DE против хода часовой стрелки, а на рис. 2 — oт стержня АЕ по ходу часовой стрелки).
Построение чертежа начинать со стержня, направление которого определяется углом α; ползун В и его направляющие для большей наглядности изобразить, как в примере К2 (см. рис. К2). Заданную угловую скорость считать направленной против хода часовой стрелки, а заданную скорость vB — oт точки В к b.Дано: L1=0,4 м, L2=1,2 м, L3=1,4 м, L4=0,8 м, α=30° β=120° γ=30° φ =0° θ=60° ω1=8 с-1
1.00 $ В корзину
Найти: VB, VE, ω3 -
Тарг 1980 год задача К3 вариант 40
Описание
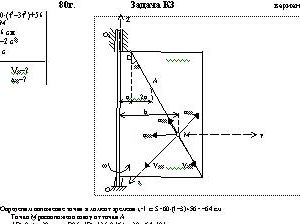
Прямоугольная пластина (рис. К3.0 — К3.5) или круглая пластина радиуса R = 60 см (рис. К3.6 — К3.9) вращается вокруг неподвижной оси с постоянной угловой скоростью ω), заданной в табл. КЗ (при знаке минус направление ω противоположно показанному на рисунке). Ось вращения на рис. 0 — 3 и 8,9 перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 4 — 7 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. 0 — 5) или по окружности радиуса R, т. е. по ободу пластины (рис. 6 — 9), движется точка М. Закон ее относительного движения, выражаемый уравнением s = AM = f(t) (s — в сантиметрах, t — в секундах), задан в табл. КЗ отдельно для рис. 0 — 5 и для рис. 6—9,
при этом на рис. 6 — 9 s = AM и отсчитывается по дуге окружности; там же даны размеры а и h. На всех рисунках точка М показана в положении, при котором s = AM > 0 (при s <0 точка М находится по другую сторону от точки А).
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 с.Дано: S=60*(t4-3t2)+56, S=AM, a=16 см, ω= -2 c-1, t=1 c
1.00 $ В корзину
Найти: VM, aM -
Тарг 1980 год задача К3 вариант 46
Описание
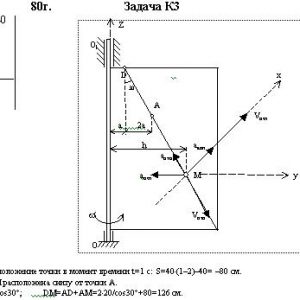
Прямоугольная пластина (рис. К3.0 — К3.5) или круглая пластина радиуса R = 60 см (рис. К3.6 — К3.9) вращается вокруг неподвижной оси с постоянной угловой скоростью ω), заданной в табл. КЗ (при знаке минус направление ω противоположно показанному на рисунке). Ось вращения на рис. 0 — 3 и 8,9 перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 4 — 7 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. 0 — 5) или по окружности радиуса R, т. е. по ободу пластины (рис. 6 — 9), движется точка М. Закон ее относительного движения, выражаемый уравнением s = AM = f(t) (s — в сантиметрах, t — в секундах), задан в табл. КЗ отдельно для рис. 0 — 5 и для рис. 6—9,
при этом на рис. 6 — 9 s = AM и отсчитывается по дуге окружности; там же даны размеры а и h. На всех рисунках точка М показана в положении, при котором s = AM > 0 (при s <0 точка М находится по другую сторону от точки А).
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 с.Дано: S=40*(t-2t3)-40, S=AM, a=20 см, ω= 4 c-1, t=1 c
1.00 $ В корзину
Найти: VM, aM -
Тарг 1980 год задача С1 вариант 50
Описание
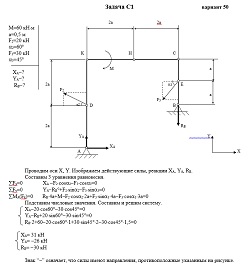
Жесткая рама (рис. С 1.0 — С 1.9, табл. С1) закреплена в точке А шарнирно, а в точке В прикреплена или к невесомому стержню ВВ1 или к шарнирной опоре на катках; стержень прикреплен к раме и к неподвижной опоре шарнирами.
На раму действуют пара сил с моментом М = 60 Н*м и две силы, величины которых, направления и точки, приложения указаны в таблице (например, в условиях № 1 на раму действуют сила F1 = 10 Н под углом 30° к горизонтальной оси, приложенная а точке К, и сила F4 = 40 Н под углом 60° к горизонтальной оси, приложенная в точке Н).
Определить реакции связей в точках А и В, вызываемые заданными нагрузками. При окончательных подсчетах принять а = 0,5 м.Дано: М=60 кН*м, а=0,5 м, F2=20 кН, α2=60°, F3=30 кН, α3=45°
1.00 $ В корзину
Найти: XA, YA, RB -
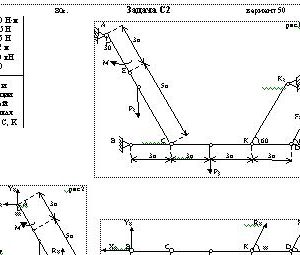
Тарг 1980 год задача С2 вариант 50
Описание
Однородные брусья АС весом Р1 = 15 Н и BD (или ВС) весом Р2 = 25 Н, расположены в вертикальной плоскости (рис. С2.0 — С2.9, табл. С2). В точке С брусья или свободно опираются друг о друга (рис. 0 — 5) или соединены шарниром (рис. 6 — 9). Внешними связями являются шарнир в точке А, невесомый стержень КК1, шарнир в точке В (на рис. 0 — 5), выступ Н (на рис. 6) и гладкая плоскость (на рис. 7 — 9 в точке В).
1.00 $ В корзину
На брусья кроме сил тяжести действуют пара сил с моментом М = 50 Н*м и сила, величина которой, направление и точка приложения указаны в табл. С2 (например, по условиям № 1 таблицы на брус действует сила F2= 20 Н, приложенная в точке Е и направленная под углом α2=30° к горизонтальной оси).
Определить реакции связей в точках А, В, С и К (на рис. 6 в точках А, С, К и Н). При окончательных расчетах принять а = 0,2 м.
Дано: M=50 Н*м, P1=15 H, P2=25 H, а=0,2 м, F1=10 кН, α1=60°
Найти: реакции связей в точках А, В, С, K -
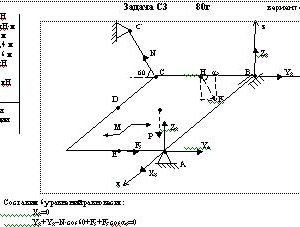
Тарг 1980 год задача С3 вариант 44
Описание
Однородная прямоугольная плита весом Р=3 кН со сторонами АВ = За, ВС = 2а закреплена в точке А сферическим, а в точке В цилиндрическим шарниром (подшипником) и удерживается в равновесии невесомым стержнем СС′ (рис. СЗ.0 — С3.9).
На плиту действуют пара сил с моментом М = 5 кН*м, лежащая в плоскости плиты, и две силы. Величины этих сил, их направления и точки приложения указаны в табл. СЗ; при этом силы F1 и F4 лежат в плоскостях, параллельных плоскости ху, сила F2 — в плоскости, параллельной хz, и сила F3 — в плоскости, параллельной уz. Точки приложения сил (D, Е, Н) находятся в серединах сторон плиты.
Определить реакции связей в точкам А, В и С. При подсчетах принять а = 0,8 м.Дано: Р=3 кН, М=5 кН*м, a=0,8 м, АВ=2,4 м, ВС=1,6 м, F2=6 кН, α2=60° F4=10 кН, α4=90°
1.00 $ В корзину
Найти: реакции опор -
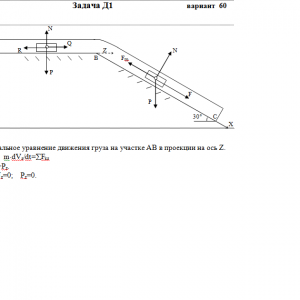
Тарг 1982 год задача Д1 вариант 60
Описание
Груз D массой m, получив в точке А начальную скорость vo, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0—Д1.9, табл. Д1).
На участке АВ на груз кроме силы тяжести действуют постоянная сила Q (ее направление показано на рисунках) и сила сопротивления среды R, зависящая от скорости v груза (направлена против движения); трением груза о трубу на участке АВ пренебречь.
В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него кроме силы тяжести действуют сила трения (коэффициент трения груза о трубу f=0,2) и переменная сила F, проекция которой Fx на ось х задана в таблице.
Считая груз материальной точкой и зная расстояние АВ=l или время t1 движения груза от точки А до точки В, найти закон движения груза па участке ВС, т. е. х=f(t), где x=BD.Дано: m=2 кг, V0=20 м/с, Q=6 Н, R=0,4V, t=2,5 c, F=2*sin(4t), f=0,2
1.00 $ В корзину
Найти: x(t) -
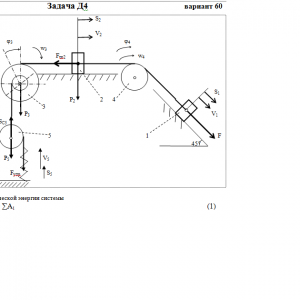
Тарг 1982 год задача Д4 вариант 60
Описание
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3=0,3 м, r3=0,l м и радиусом инерции относительно оси вращения ρ3=0,2 м, блока 4 радиуса R4=0,2 м и катка (или подвижного блока) 5 (рис. Д4.0—Д4.9, табл. Д4); тело 5 считать сплошным однородным цилиндром, а массу блока 4—равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f= 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F=f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1=0,2 м. Искомая величина указана в столбце Найти таблицы, где обозначено: v1, v2, vσ5 — скорости грузов 1, 2 и центра масс тела 5 соответственно, ω3 и ω4 — угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 1), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2=0; остальные тела должны изображаться и тогда, когда их масса равна нулю.Дано: m1=0 кг, m2=6 кг, m3=4 кг, m4=0 кг, m5=5 кг, М=1,2 Н*м, С=200 Н/м, F=80*(4+5*S), R3=0,3 м, r3=0,1 м, ρ3=0,2 м, R4=0,2 м, f=0,1
1.00 $ В корзину
Найти: ω3 -

Тарг 1982 год задача К1 вариант 60
Описание
Точка В движется в плоскости ху (рис. К 1.0—К 1.9, табл. К1; траектория точки на рисунках показана условно). Закон движения точки задан уравнениями x=f1(t), y=f2(t), где х и у выражены в сантиметрах, t — в секундах.
1.00 $ В корзину
Найти уравнение траектории точки; для момента времени t1 = 1 с определить скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Зависимость x=f1(t) указана непосредственно на рисунках, а зависимость y=f2(t) дана в табл. К1 (для рис. 0—2 в столбце 2, для рис. 3—6 в столбце 3, для рис. 7—9 в столбце 4). Как и в задачах Cl—С5, номер рисунка выбирается по предпоследней цифре шифра, а номер условия в табл. К1 — по последней. -
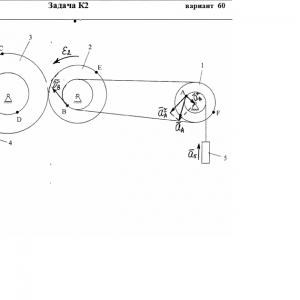
Тарг 1982 год задача К2 вариант 60
Описание
Механизм состоит из ступенчатых колее 1—3, находящихся в зацеплении или связанных ременной передачей, зубчатой рейки 4 и груза 5, привязанного к концу нити, намотанной на одно из колес (рис. К2.0—К2.9, табл. К2). Радиусы ступеней колес равны соответственно; у колеса 1 — г1=2 см, R1=4 см, у колеса 2 — r2=6 см, R2=8 см, у колеса 3 — r3=12 см, R3=16 см. На ободьях колес расположены точки А, В и С.
1.00 $ В корзину
В столбце Дано таблицы указан закон движения или закон изменения скорости ведущего звена механизма, где φ1(t) — закон вращения колеса 1, s4(t) — закон движения рейки 4, ω2(t) — закон изменения угловой скорости колеса 2, v5(t) — закон изменения скорости груза 5 и т. д. (везде φ выражено в радианах, s — в сантиметрах, t — в секундах). Положительное направление для φ и ω против хода часовой стрелки, для S4, S5 и v4, v5 — вниз.
Определить в момент времени t1=2 с указанные в таблице в столбцах Найти скорости (v — линейные, ω — угловые) и ускорения (а — линейные, ε — угловые) соответствующих точек или тел (v5 — скорость груза 5 и т. д.). -
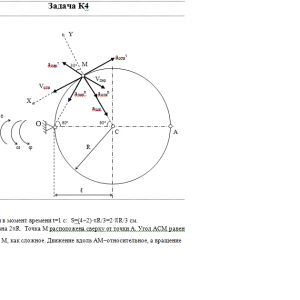
Тарг 1982 год задача К4 вариант 60
Описание
Прямоугольная пластина (рис. К4.0—К4.4) или круглая пластина радиуса R=60 см (рис. К4.5—К4.9) вращается вокруг неподвижной оси но закону φ=f1(t) заданному в табл. К4. Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. На рис. О, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3, 4, 7, 8, 9 ось вращения OO1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD (рис. О—4) или по окружности радиуса R (рис. 5—9) движется точка М; закон ее относительного движения, т. е. зависимость s=AM=f2(t) (s выражено в сантиметрах, t—в секундах), задан в таблице отдельно для рис. 0—4 и для рис. 5—9; там же даны размеры b и l. На рисунках точка М показана в положении, при котором s=AM>0 (при s<0 точка М находится по другую сторону от точки А).
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1 = 1 с.Дано: φ=4(t2-t), ℓ=R, S=AM, S=(4*t2-t3)*πR/3, t=1 c, R=60 см
1.00 $ В корзину
Найти: VM, aM -
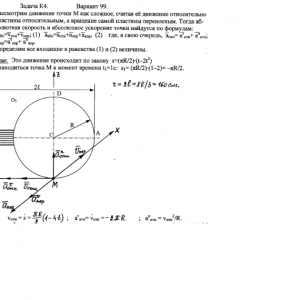
Тарг 1982 год задача К4 вариант 99
Описание
Прямоугольная пластина (рис. К4.0—К4.4) или круглая пластина радиуса R = 60 см (рис. К4.5—К4.9) вращается вокруг неподвижной оси по закону φ=f1(t), заданному в табл. К4. Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. На рис. О, 1, 2, 5, 6 ось вращения перпендикулярна плоскости пластины и проходит через точку О (пластина вращается в своей плоскости); на рис. 3. 4, 7, 8, 9 ось вращения ОО1 лежит в плоскости пластины (пластина вращается в пространстве).
1.00 $ В корзину
По пластине вдоль прямой BD (рис. 0—4) или по окружности радиуса R (рис. 5—9) движется точка М; закон ее относительного движения, т. е. зависимость s=AM=f2(t) (s выражено в сантиметрах, t—в секундах), задан в таблице отдельно для рис. 0—4 н для рис. 5—9; там же даны размеры b и l. На рисунках точка М показана в положении, при котором s=АМ>0 (при s<0 точка М находится по другую сторону от точки А).
Найти абсолютную скорость и абсолютное ускорение точки М в момент времени t1=l с.