Теоретическая механика Тарга 80 год
Отображение 65–96 из 153
-
Тарг 1980 год задача Д2 вариант 89
Описание
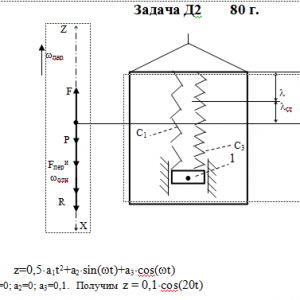
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону
z =1/2*a1t2+a2*sin(ωt)+a3*cos(ωt)
(ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R =μv, где v— скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т.е. х = f(t): начало координат поместить в положении статического равновесия груза при неподвижном лифте. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3—коэффициенты жесткости пружин, λст— статическое удлинение пружины с эквивалентной жесткостью, λ0 — удлинение пружины с эквивалентной жесткостью в начальный момент времени t0= 0, v0—начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк во всех столбцах с1 с2, с3 стоит, когда задано λст (пружину с эквивалентной жесткостью считать в этом случае прикрепленной к потолку лифта), а прочерк в одном из столбцов означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин. Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=0,5 кг, C1=180 Н/м, С2=120 Н/м, a1=0 м/с2, a2=0 м, a3=0,1 м, ω=20 с-1, μ=0 Н*с/м, λ0=0 м, V0=0 м/с
1.00 $ В корзину
Найти: x(t) -
Тарг 1980 год задача Д2 вариант 90
Описание
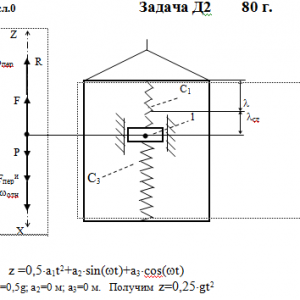
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону
z =1/2*a1t2+a2*sin(ωt)+a3*cos(ωt)
(ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R =μv, где v— скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т.е. х = f(t): начало координат поместить в положении статического равновесия груза при неподвижном лифте. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3—коэффициенты жесткости пружин, λст— статическое удлинение пружины с эквивалентной жесткостью, λ0 — удлинение пружины с эквивалентной жесткостью в начальный момент времени t0= 0, v0—начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк во всех столбцах с1 с2, с3 стоит, когда задано λст (пружину с эквивалентной жесткостью считать в этом случае прикрепленной к потолку лифта), а прочерк в одном из столбцов означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин. Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=0,5 кг, C1=80 Н/м, C3=120 Н/м, a1=0,5g м/с2, a2=0 м, a3=0 м, μ=12 Н*с/м, λ0=0 м, V0=4 м/с
1.00 $ В корзину
Найти: x(t) -
Тарг 1980 год задача Д2 вариант 92
Описание
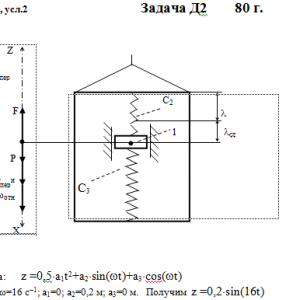
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону
z =1/2*a1t2+a2*sin(ωt)+a3*cos(ωt)
(ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R =μv, где v— скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т.е. х = f(t): начало координат поместить в положении статического равновесия груза при неподвижном лифте. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3—коэффициенты жесткости пружин, λст— статическое удлинение пружины с эквивалентной жесткостью, λ0 — удлинение пружины с эквивалентной жесткостью в начальный момент времени t0= 0, v0—начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк во всех столбцах с1 с2, с3 стоит, когда задано λст (пружину с эквивалентной жесткостью считать в этом случае прикрепленной к потолку лифта), а прочерк в одном из столбцов означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин. Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=1 кг, с2=160 Н/м, с3=240 Н/м, a1=0 м/с2, a2=0,2 м, a3=0 м, ω=16 с-1 μ=0 Н*с/м, λ0=0,15 м, V0=0 м/с
1.00 $ В корзину
Найти: x(t) -
Тарг 1980 год задача Д2 вариант 94
Описание
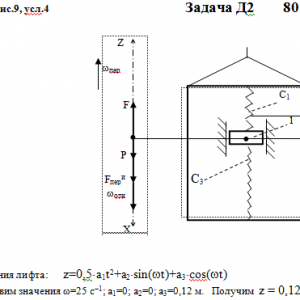
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону
z =1/2*a1t2+a2*sin(ωt)+a3*cos(ωt)
(ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R =μv, где v— скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т.е. х = f(t): начало координат поместить в положении статического равновесия груза при неподвижном лифте. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3—коэффициенты жесткости пружин, λст— статическое удлинение пружины с эквивалентной жесткостью, λ0 — удлинение пружины с эквивалентной жесткостью в начальный момент времени t0= 0, v0—начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк во всех столбцах с1 с2, с3 стоит, когда задано λст (пружину с эквивалентной жесткостью считать в этом случае прикрепленной к потолку лифта), а прочерк в одном из столбцов означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин. Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=0,5 кг, с1=150 Н/м, с3=300 Н/м, a1=0 м/с2, a2=0 м, a3=0,12 м, ω=25 с-1 μ=0 Н*с/м, λ0=0 м, V0=0 м/с
1.00 $ В корзину
Найти: x(t) -
Тарг 1980 год задача Д2 вариант 95
Описание
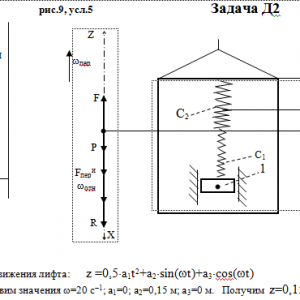
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону
z =1/2*a1t2+a2*sin(ωt)+a3*cos(ωt)
(ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R =μv, где v— скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т.е. х = f(t): начало координат поместить в положении статического равновесия груза при неподвижном лифте. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3—коэффициенты жесткости пружин, λст— статическое удлинение пружины с эквивалентной жесткостью, λ0 — удлинение пружины с эквивалентной жесткостью в начальный момент времени t0= 0, v0—начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк во всех столбцах с1 с2, с3 стоит, когда задано λст (пружину с эквивалентной жесткостью считать в этом случае прикрепленной к потолку лифта), а прочерк в одном из столбцов означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин. Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=0,4 кг, с1=50 Н/м, с2=200 Н/м, a1=0 м/с2, a2=0,15 м, a3=0 м, ω=20 с-1 μ=0 Н*с/м, λ0=0 м, V0=0 м/с
1.00 $ В корзину
Найти: x(t) -
Тарг 1980 год задача Д2 вариант 97
Описание
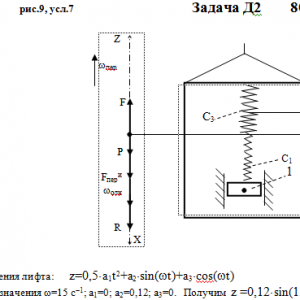
Груз 1 массой m укреплен на пружинной подвеске в лифте (рис. Д2.0 — Д2.9, табл. Д2). Лифт движется вертикально по закону
z =1/2*a1t2+a2*sin(ωt)+a3*cos(ωt)
(ось z направлена по вертикали вверх; z выражено в метрах, t — в секундах). На груз действует сила сопротивления среды R =μv, где v— скорость груза по отношению к лифту.
Найти закон движения груза по отношению к лифту, т.е. х = f(t): начало координат поместить в положении статического равновесия груза при неподвижном лифте. При подсчетах можно принять g = 10 м/с2. Массой пружин и соединительной планки 2 пренебречь.
В таблице обозначено: с1, с2, с3—коэффициенты жесткости пружин, λст— статическое удлинение пружины с эквивалентной жесткостью, λ0 — удлинение пружины с эквивалентной жесткостью в начальный момент времени t0= 0, v0—начальная скорость груза по отношению к лифту (направлена вертикально вверх). Прочерк во всех столбцах с1 с2, с3 стоит, когда задано λст (пружину с эквивалентной жесткостью считать в этом случае прикрепленной к потолку лифта), а прочерк в одном из столбцов означает, что соответствующая пружина отсутствует и на чертеже изображаться не должна. Если при этом конец одной из оставшихся пружин окажется свободным, его следует прикрепить в соответствующем месте или к грузу или к потолку (полу) лифта; то же следует сделать, если свободными окажутся соединенные планкой 2 концы обеих оставшихся пружин. Условие μ = 0 означает, что сила сопротивления R отсутствует.Дано: m=2 кг, с1=400 Н/м, с3=400 Н/м, a1=0, a2=0,12 м, a3=0, ω=15 с-1 μ=0 Н*с/м, λ0=0 м, V0=0 м/с
1.00 $ В корзину
Найти: x(t) -
Тарг 1980 год задача Д4 вариант 44
Описание
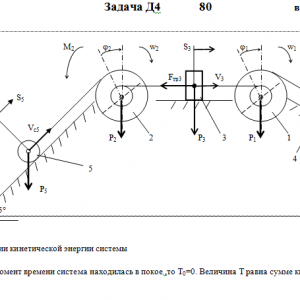
Механическая система состоит из ступенчатых шкивов 1 и 2 с радиусами ступеней R1=0,3 м, r1=0,1 м, R2=0,2 м, r2=0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу), грузов 3 и 4 (коэффициент трения скольжения грузов о плоскость f = 0,1) и цилиндрического сплошного однородного катка 5 (рис. Д4.0—Д4.9, табл. Д4). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям.
Под действием силы F=f(S), зависящей от перемещения S точки приложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 1 и 2 действуют постоянные моменты сил сопротивлений, равные соответственно М1 и М2.
Определить значение искомом величины в тот момент времени, когда перемещение точки приложения силы F равно S1. Искомая величина указана в столбце Найти таблицы, где обозначено: ω1 -угловая скорость тела 1, v3 — скорость груза 3, vС5 — скорость центра масс катка 5 и т.д.Дано: m1=4 кг, m2=0 кг , m3=8 кг, m4=0 кг, m5=2 кг, М1=0 Н*м, M2=0,6 Н*м, F=60(1+2*S), R1=0,3 м, r1=0,1 м, R2=0,2 м, r2=0,1 м, f=0,1, S1=1,4 м
1.00 $ В корзину
Найти: ω1 -
Тарг 1980 год задача Д4 вариант 79
Описание
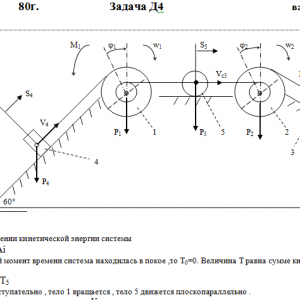
Механическая система состоит из ступенчатых шкивов 1 и 2 с радиусами ступеней R1=0,3 м, r1=0,1 м, R2=0,2 м, r2=0,1 м (массу каждого шкива считать равномерно распределенной по его внешнему ободу), грузов 3 и 4 (коэффициент трения скольжения грузов о плоскость f = 0,1) и цилиндрического сплошного однородного катка 5 (рис. Д4.0—Д4.9, табл. Д4). Тела системы соединены друг с другом нитями, намотанными на шкивы; участки нитей параллельны соответствующим плоскостям.
Под действием силы F=f(S), зависящей от перемещения S точки приложения силы, система приходит в движение из состояния покоя. При движении системы на шкивы 1 и 2 действуют постоянные моменты сил сопротивлений, равные соответственно М1 и М2.
Определить значение искомом величины в тот момент времени, когда перемещение точки приложения силы F равно S1. Искомая величина указана в столбце Найти таблицы, где обозначено: ω1 -угловая скорость тела 1, v3 — скорость груза 3, vС5 — скорость центра масс катка 5 и т.д.Дано: m1=2 кг, m2=0 кг , m3=4 кг, m4=0 кг, m5=6 кг, М1=0 Н*м, M2=0,4 Н*м, F=80*(1+S), R1=0,3 м, r1=0,1 м, R2=0,2 м, r2=0,1 м, f=0,1, S1=1,4 м
1.00 $ В корзину
Найти: V3 -
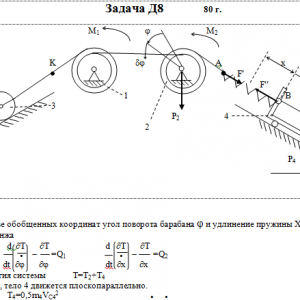
Тарг 1980 год задача Д8 вариант 01
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P5=0, P4=3P, F=P, M1=0, M2=0, пружина AB Найти: Составить уравнения Лагранжа, k-?, τ-? -
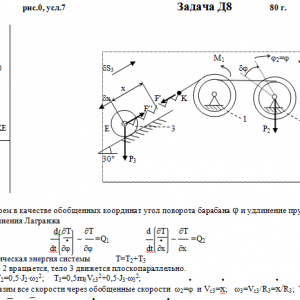
Тарг 1980 год задача Д8 вариант 07
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P4=P5=0, P2=2P, P3=P, F=0, M1=0, M2= -2PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
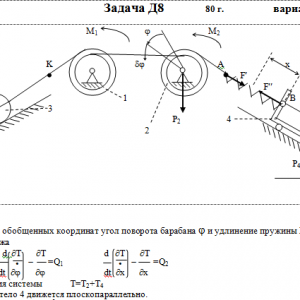
Тарг 1980 год задача Д8 вариант 08
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=P, P3=P5=0, P4=2P, F=0, M1=3PR, M2=0, пружина AB Найти: Составить уравнения Лагранжа, k-?, τ-? -
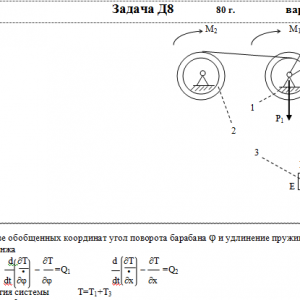
Тарг 1980 год задача Д8 вариант 10
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=P, F=0, M1=0, M2= -3PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -

Тарг 1980 год задача Д8 вариант 12
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=P, P3=P4=0, P5=2P, F=0, M1=2PR, M2=0, пружина AD Найти: Составить уравнения Лагранжа, k-?, τ-? -
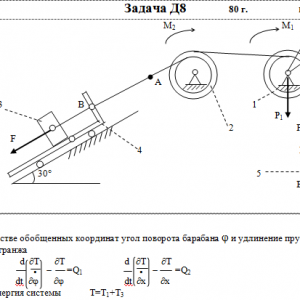
Тарг 1980 год задача Д8 вариант 14
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=2P, P4=P5=0, F=0, M1= -3PR, M2=0, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
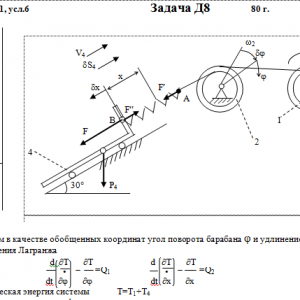
Тарг 1980 год задача Д8 вариант 16
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=P5=0, P4=2P, F=0, M1=2PR, M2=0, пружина AB Найти: Составить уравнения Лагранжа, k-?, τ-? -
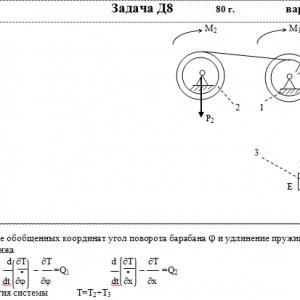
Тарг 1980 год задача Д8 вариант 17
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P, P4=P5=0, F=0, M1=0, M2= -2PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
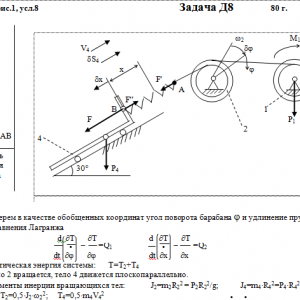
Тарг 1980 год задача Д8 вариант 18
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=Р, P3=P5=0, P4=2P, F=0, M1=3PR, M2=0, пружина AB Найти: Составить уравнения Лагранжа, k-?, τ-? -
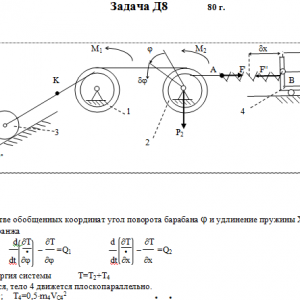
Тарг 1980 год задача Д8 вариант 21
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P5=0, P4=3P, F=P, M1=0, M2=0, пружина AB Найти: Составить уравнения Лагранжа, k-?, τ-? -
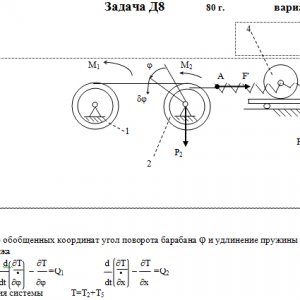
Тарг 1980 год задача Д8 вариант 22
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=P, P3=P4=0, P5=2P, F=0, M1=2PR, M2=0, пружина AD Найти: Составить уравнения Лагранжа, k-?, τ-? -
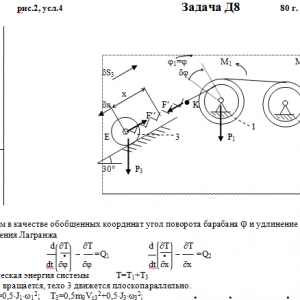
Тарг 1980 год задача Д8 вариант 24
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P2=P4=P5=0, P1=P, P3=2P, F=0, M1= -3PR, M2=0, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
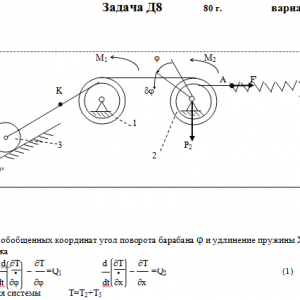
Тарг 1980 год задача Д8 вариант 25
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P4=0, P5=P, F=0, M1=0, M2=4PR, пружина AD Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 26
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
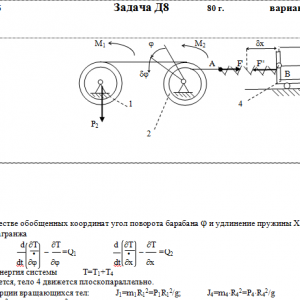
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=P5=0, P4=2*P, F=0, M1=2*PR, M2=0, пружина AB Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 27
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
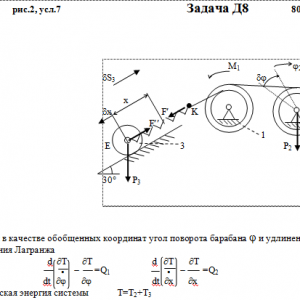
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P4=P5=0, P2=2P, P3=P, F=0, M1=0, M2= -2PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 29
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
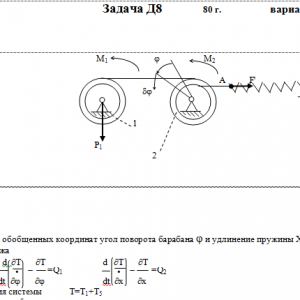
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=2P, P2=0, P3=P4=0, P5=P, F=3P, M1=0, M2=0, пружина AD Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 30
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
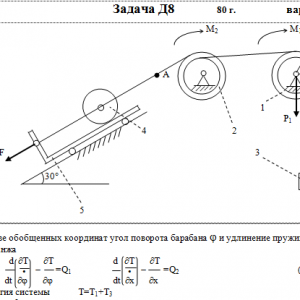
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=P, F=0, M1=0, M2= -3PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
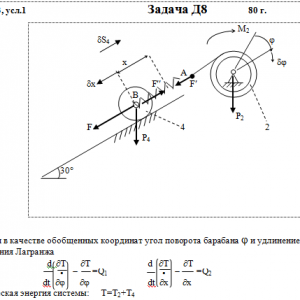
Тарг 1980 год задача Д8 вариант 31
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P5=0, P4=3P, F=P, M1=0, M2=0, пружина AB Найти: Составить уравнения Лагранжа, k-?, τ-? -
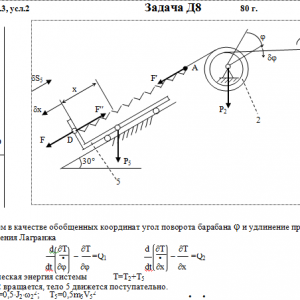
Тарг 1980 год задача Д8 вариант 32
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=P, P3=P4=0, P5=2P, F=0, M1=2PR, M2=0, пружина AD Найти: Составить уравнения Лагранжа, k-?, τ-? -
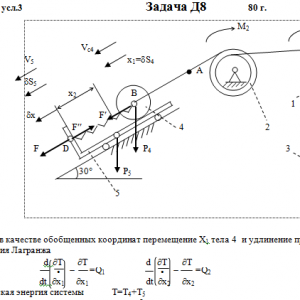
Тарг 1980 год задача Д8 вариант 33
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P2=P3=0, P4=3P, P5=2P, F=P, M1=0, M2=0, пружина BD Найти: Составить уравнения Лагранжа, k-?, τ-? -
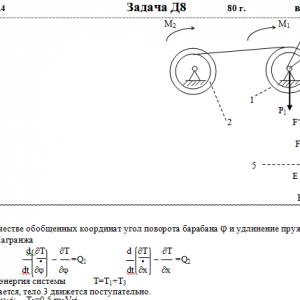
Тарг 1980 год задача Д8 вариант 34
Описание
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=2P, P4=P5=0, F=0, M1= -3PR, M2=0, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 35
Описание
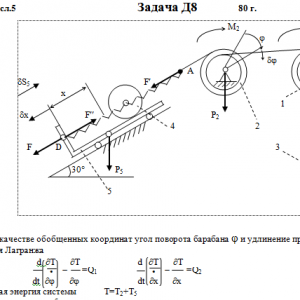
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P4=0, P5=P, F=0, M1=0, M2=4PR, пружина AD Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 36
Описание
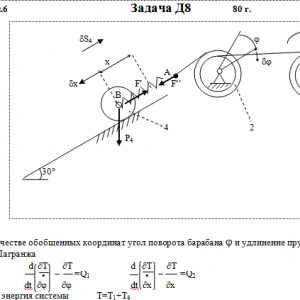
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=P, P2=0, P3=P5=0, P4=2P, F=0, M1=2PR, M2=0, пружина AB Найти: Составить уравнения Лагранжа, k-?, τ-? -
Тарг 1980 год задача Д8 вариант 37
Описание
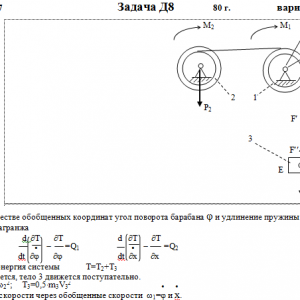
Механическая система состоит из тел 1, 2, …. 5 весом Р1, Р2,…, Р5, связанных нитями, намотанными на ступенчатые блоки 1 и 2 (рис. Д8.0 — Д8.9, табл. Д8). Прочерк в столбцах таблицы, где заданы веса, означает, что соответствующее тело в систему не входит (на чертеже не изображать), а ноль — что тело считается невесомым, но в систему входит.
1.00 $ В корзину
Радиусы ступенчатых блоков 1 и 2 равны соответственно: R1=R, r1=0,8R, R2=R, r2=0,4R. При вычислении моментов инерции оба блока и катки считать однородными цилиндрами радиуса R.
На систему кроме сил тяжести действуют сила F, приложенная к телу 4 или 5 (или к соответствующему концу нити, когда тело в систему не входит), и пары с моментами М1 и М2, приложенные к блокам, при М<0 направление момента противоположно показанному на рисунке. На участке нити, указанном в таблице в столбце Пружина, включена пружина с коэффициентом жесткости с (например, если в столбце стоит АВ, то участок АВ является пружиной, если АD, то АD—пружина, и т. д.); в начальный момент времени пружины не деформированы. Составить для системы уравнения Лагранжа и определить из них частоту и период колебаний, совершаемых телами системы при ее движении. Если в решаемом варианте задачи тележка в систему не входит (ее вес в таблице прочеркнут), а вес лежащего на ней катка 4 (или 5) задан, то этот каток следует считать движущимся по плоскости, на которой в исходном рисунке стоит тележка (тележку не изображать, а плоскость приподнять до касания с катком, т. е., например, изобразить каток и плоскость так, как это показано на рис. Д8.10 для катка 4. Дано: R1=R, r1=0,8R, R2=R, r2=0,4R, P1=0, P2=2P, P3=P, P4=P5=0, F=0, M1=0, M2= -2PR, пружина KE Найти: Составить уравнения Лагранжа, k-?, τ-?