Магазин

Отображение 321–352 из 3934

• 

  Детали машин задачи группа 4 вариант 8

  Описание

  1.Рассчитать механизм подъема поворотного крана
  Вес груза F=90 кН, скорость подъема груза v=9 м/мин (0,15 м/с), высота подъема груза Н=8 м, режим работы – 5М.
  Требуется:
  1) определить мощность электродвигателя и подобрать его по каталогу;
  2) определить общее передаточное число механизма подъема, выбрать тип передач, сделать кинематический расчет;
  3) выбрать тип тормоза произвести его расчет и подобрать по каталогу электромагнит;
  4) рассчитать канат и подобрать его по ГОСТ-ИСО;
  5) определить диаметр, длину, канатоемкость и толщину стенок барабана и проверить барабан на прочность;
  6) определить диаметры блоков;
  7) выбрать по ГОСТу крюк.

  2. Рассчитать ленточный конвейер
  Расчетная часовая производительность конвейера Q=230 т/ч
  Насыпная плотность транспортируемого материала ρ=1,6 т/м3,
  Длины участков по горизонтали l1=48м; l2=33м;
  Угол наклона конвейера 12
  Скорость транспортируемого материала v= 2,2 м/с.
  Требуется:
  1) определить ширину ленты с округлением ее до ближайшей стандартной;
  2) вычислить силы сопротивления движению ленты на всех участках конвейера;
  3) определить силы натяжения ленты и тяговое усилие на приводном барабане;
  4) по максимальному натяжению ленты определить число прокладок и толщину ее;
  5) выбрать конструкцию поддерживающих роликов и барабанов и определить их диаметры;
  6) определить мощность электродвигателя и подобрать его по каталогу;
  7) определить общее передаточное число привода конвейера, наметить тип передач и определить передаточное число каждой передачи

  Методичка здесь
  метод задачи к контрольным заданиям Меновщиков В.А

  1.00 $ В корзину
• 

  Детали машин задачи группа 5 вариант 3

  Описание

  1. Рассчитать механизм подъема железнодорожного кра¬на
  Вес груза F=40 кН, скорость подъема груза v=10 м/мин (0,166 м/с), высота подъема груза Н=10 м, режим работы – 3М.
  Требуется:
  1) определить мощность электродвигателя и подобрать его по каталогу;
  2) определить общее передаточное число механизма подъема, выбрать тип передач, сделать кинематический расчет;
  3) выбрать тип тормоза произвести его расчет и подобрать по каталогу электромагнит;
  4) рассчитать канат и подобрать его по ГОСТ-ИСО;
  5) определить диаметр, длину, канатоемкость и толщину стенок барабана и проверить барабан на прочность;
  6) определить диаметры блоков;
  7) выбрать по ГОСТу крюк.

  2. Рассчитать ленточный конвейер
  Расчетная часовая производительность конвейера Q=360 т/ч
  Насыпная плотность транспортируемого материала ρ=2,4 т/м3,
  Длины участков по горизонтали l1=36м; l2=44м;
  Угол наклона конвейера 15
  Скорость транспортируемого материала v=1,3 м/с.
  Требуется:
  1) определить ширину ленты с округлением ее до ближайшей стандартной;
  2) вычислить силы сопротивления движению ленты на всех участках конвейера;
  3) определить силы натяжения ленты и тяговое усилие на приводном барабане;
  4) по максимальному натяжению ленты определить число прокладок и толщину ее;
  5) выбрать конструкцию поддерживающих роликов и барабанов и определить их диаметры;
  6) определить мощность электродвигателя и подобрать его по каталогу;
  7) определить общее передаточное число привода конвейера, наметить тип передач и определить передаточное число каждой передачи

  Методичка здесь
  метод задачи к контрольным заданиям Меновщиков В.А

  1.00 $ В корзину
• 

  Детали машин задачи группа 6 вариант 3

  Описание

  1. Рассчитать механизм подъема велосипедного крана
  Вес груза F=8 кН, скорость подъема груза v=6 м/мин (0,1 м/с), высота подъема груза Н=4 м, режим работы – 5М.
  Требуется:
  1) определить мощность электродвигателя и подобрать его по каталогу;
  2) определить общее передаточное число механизма подъема, выбрать тип передач, сделать кинематический расчет;
  3) выбрать тип тормоза произвести его расчет и подобрать по каталогу электромагнит;
  4) рассчитать канат и подобрать его по ГОСТ-ИСО;
  5) определить диаметр, длину, канатоемкость и толщину стенок барабана и проверить барабан на прочность;
  6) определить диаметры блоков;
  7) выбрать по ГОСТу крюк.

  2. Рассчитать пластинчатый конвейер для перемещения угля
  Длины участков по горизонтали: l1 = 30 м, l2 = 45 м, l3 = 24 м, угол β=π/16 рад = 11,25
  Требуется:
  1) определить конструктивные параметры несущего полотна кон¬вейера;
  2) вычислить силы сопротивления движению несущего полотна на всех участках конвейера;
  3) определить силы натяжения тяговой цепи и тяговое уси¬лие на приводной звездочке;
  4) по максимальному натяжению выбрать тяговый орган конвейера;
  5) выбрать конструкции направляющих роликов и приводную звездочку, определить их диаметры;
  6) определить мощность электродвигателя;
  7) определить общее передаточное число привода конвейера; наметить тип пере¬дач и определить передаточное число каждой передачи.
  Исходные данные:
  Q=300 – часовая продуктивность конвейера, т/ч;
  Насыпная плотность материала ρ=0,8т/м³
  l1 = 26 м, l2 = 35, l3 = 60 м,
  Угол наклона конвейера 12
  Скорость транспортируемого материала v=0,5 м/с.

  Методичка здесь
  метод задачи к контрольным заданиям Меновщиков В.А

  1.00 $ В корзину
• 

  Детали машин задачи группа 6 вариант 8

  Описание

  1. Рассчитать механизм подъема велосипедного крана
  Вес груза F=12 кН, скорость подъема груза v=8 м/мин (0,1 м/с), высота подъема груза Н=6 м, режим работы – 3М.
  Требуется:
  1) определить мощность электродвигателя и подобрать его по каталогу;
  2) определить общее передаточное число механизма подъема, выбрать тип передач, сделать кинематический расчет;
  3) выбрать тип тормоза произвести его расчет и подобрать по каталогу электромагнит;
  4) рассчитать канат и подобрать его по ГОСТ-ИСО;
  5) определить диаметр, длину, канатоемкость и толщину стенок барабана и проверить барабан на прочность;
  6) определить диаметры блоков;
  7) выбрать по ГОСТу крюк.

  2. Рассчитать пластинчатый конвейер для перемещения угля
  Требуется:
  1) определить конструктивные параметры несущего полотна кон¬вейера;
  2) вычислить силы сопротивления движению несущего полотна на всех участках конвейера;
  3) определить силы натяжения тяговой цепи и тяговое уси¬лие на приводной звездочке;
  4) по максимальному натяжению выбрать тяговый орган конвейера;
  5) выбрать конструкции направляющих роликов и приводную звездочку, определить их диаметры;
  6) определить мощность электродвигателя;
  7) определить общее передаточное число привода конвейера; наметить тип пере¬дач и определить передаточное число каждой передачи.
  Исходные данные:
  Q=250 – расчетная часовая производительность конвейера, т/ч;
  Плотность транспортируемого материала ρ=0,9т/м³
  Длины участков по горизонтали l1 = 31 м, l2 = 35, l3 = 50 м,
  Угол наклона конвейера угол β=π/12 рад
  Скорость транспортируемого материала v=0,6 м/с.

  Методичка здесь
  метод задачи к контрольным заданиям Меновщиков В.А

  1.00 $ В корзину
• 

  Детали машин задачи группа 6 вариант 9

  Описание

  1. Рассчитать механизм подъема велосипедного крана
  Вес груза F=12 кН, скорость подъема груза v=9 м/мин, высота подъема груза Н=6 м, режим работы – 5М.
  Требуется:
  1) определить мощность электродвигателя и подобрать его по каталогу;
  2) определить общее передаточное число механизма подъема, выбрать тип передач, сделать кинематический расчет;
  3) выбрать тип тормоза произвести его расчет и подобрать по каталогу электромагнит;
  4) рассчитать канат и подобрать его по ГОСТ-ИСО;
  5) определить диаметр, длину, канатоемкость и толщину стенок барабана и проверить барабан на прочность;
  6) определить диаметры блоков;
  7) выбрать по ГОСТу крюк.

  2. Рассчитать пластинчатый конвейер для перемещения угля
  Требуется:
  1) определить конструктивные параметры несущего полотна кон¬вейера;
  2) вычислить силы сопротивления движению несущего полотна на всех участках конвейера;
  3) определить силы натяжения тяговой цепи и тяговое уси¬лие на приводной звездочке;
  4) по максимальному натяжению выбрать тяговый орган конвейера;
  5) выбрать конструкции направляющих роликов и приводную звездочку, определить их диаметры;
  6) определить мощность электродвигателя;
  7) определить общее передаточное число привода конвейера; наметить тип передач и определить передаточное число каждой передачи.
  Исходные данные:
  Q=240 – расчетная часовая производительность конвейера, т/ч;
  Плотность транспортируемого материала ρ=0,9т/м³
  Длины участков по горизонтали l1 = 32 м, l2 = 40, l3 = 60 м,
  Угол наклона конвейера угол β=π/15 рад
  Скорость транспортируемого материала v=0,5 м/с.

  Методичка здесь
  метод задачи к контрольным заданиям Меновщиков В.А

  1.00 $ В корзину
• 

  Детали машин задачи группа 7 вариант 10

  Описание

  1. Рассчитать механизм подъема настенного консольного передвижного кра¬на
  Вес груза F=17 кН, скорость подъема груза v=10 м/мин (0,167 м/с), высота подъема груза Н=7 м, режим работы – 4М.
  Требуется:
  1) определить мощность электродвигателя и подобрать его по каталогу;
  2) определить общее передаточное число механизма подъема, выбрать тип передач, сделать кинематический расчет;
  3) выбрать тип тормоза произвести его расчет и подобрать по каталогу электромагнит;
  4) рассчитать канат и подобрать его по ГОСТ-ИСО;
  5) определить диаметр, длину, канатоемкость и толщину стенок барабана и проверить барабан на прочность;
  6) определить диаметры блоков;
  7) выбрать по ГОСТу крюк.

  2. Рассчитать ленточный конвейер
  Расчетная часовая производительность конвейера Q=300 т/ч
  Насыпная плотность транспортируемого материала ρ=1,9т/м³
  Длины участков по горизонтали l1=25м; l2=18м; l3=30м
  Угол наклона конвейера β=15
  Скорость транспортируемого материала v=1,9 м/с.
  Требуется:
  1) определить ширину ленты с округлением ее до ближайшей стандартной;
  2) вычислить силы сопротивления движению ленты на всех участках конвейера;
  3) определить силы натяжения ленты и тяговое усилие на приводном барабане;
  4) по максимальному натяжению ленты определить число прокладок и толщину ее;
  5) выбрать конструкцию поддерживающих роликов и барабанов и определить их диаметры;
  6) определить мощность электродвигателя и подобрать его по каталогу;
  7) определить общее передаточное число привода конвейера, наметить тип передач и определить передаточное число каждой передачи

  Методичка здесь
  метод задачи к контрольным заданиям Меновщиков В.А

  1.00 $ В корзину
• 

  Детали машин задачи группа 7 вариант 4

  Описание

  1. Рассчитать механизм подъема настенного консольного передвижного кра¬на
  Вес груза F=11 кН, скорость подъема груза v=8 м/мин (0,133 м/с), высота подъема груза Н=5 м, режим работы – 4М.
  Требуется:
  1) определить мощность электродвигателя и подобрать его по каталогу;
  2) определить общее передаточное число механизма подъема, выбрать тип передач, сделать кинематический расчет;
  3) выбрать тип тормоза произвести его расчет и подобрать по каталогу электромагнит;
  4) рассчитать канат и подобрать его по ГОСТ-ИСО;
  5) определить диаметр, длину, канатоемкость и толщину стенок барабана и проверить барабан на прочность;
  6) определить диаметры блоков;
  7) выбрать по ГОСТу крюк.

  2. Рассчитать ленточный конвейер
  Расчетная часовая производительность конвейера Q=240 т/ч
  Насыпная плотность транспортируемого материала ρ=1,8т/м³
  Длины участков по горизонтали l1=19м; l2=18м; l3=24м
  Угол наклона конвейера 15
  Скорость транспортируемого материала v=1,8 м/с.
  Требуется:
  1) определить ширину ленты с округлением ее до ближайшей стандартной;
  2) вычислить силы сопротивления движению ленты на всех участках конвейера;
  3) определить силы натяжения ленты и тяговое усилие на приводном барабане;
  4) по максимальному натяжению ленты определить число прокладок и толщину ее;
  5) выбрать конструкцию поддерживающих роликов и барабанов и определить их диаметры;
  6) определить мощность электродвигателя и подобрать его по каталогу;
  7) определить общее передаточное число привода конвейера, наметить тип передач и определить передаточное число каждой передачи

  Методичка здесь
  метод задачи к контрольным заданиям Меновщиков В.А

  1.00 $ В корзину
• 

  Детали машин задачи группа 7 вариант 5

  Описание

  1. Рассчитать механизм подъема настенного консольного передвижного кра¬на
  Вес груза F=12 кН, скорость подъема груза v=9 м/мин (0,15 м/с), высота подъема груза Н=5 м, режим работы – 2М.
  Требуется:
  1) определить мощность электродвигателя и подобрать его по каталогу;
  2) определить общее передаточное число механизма подъема, выбрать тип передач, сделать кинематический расчет;
  3) выбрать тип тормоза произвести его расчет и подобрать по каталогу электромагнит;
  4) рассчитать канат и подобрать его по ГОСТ-ИСО;
  5) определить диаметр, длину, канатоемкость и толщину стенок барабана и проверить барабан на прочность;
  6) определить диаметры блоков;
  7) выбрать по ГОСТу крюк.

  2. Рассчитать ленточный конвейер
  Расчетная часовая производительность конвейера Q=250 т/ч
  Насыпная плотность транспортируемого материала ρ=1,8т/м³
  Длины участков по горизонтали l1=20м; l2=16м; l3=25м
  Угол наклона конвейера β=18
  Скорость транспортируемого материала v=1,9 м/с.
  Требуется:
  1) определить ширину ленты с округлением ее до ближайшей стандартной;
  2) вычислить силы сопротивления движению ленты на всех участках конвейера;
  3) определить силы натяжения ленты и тяговое усилие на приводном барабане;
  4) по максимальному натяжению ленты определить число прокладок и толщину ее;
  5) выбрать конструкцию поддерживающих роликов и барабанов и определить их диаметры;
  6) определить мощность электродвигателя и подобрать его по каталогу;
  7) определить общее передаточное число привода конвейера, наметить тип передач и определить передаточное число каждой передачи

  Методичка здесь
  метод задачи к контрольным заданиям Меновщиков В.А

  1.00 $ В корзину
• 

  Детали машин задачи группа 8 вариант 5

  Описание

  1. Рассчитать механизм подъема консольного поворотного крана
  Вес груза F=20 кН, скорость подъема груза v=7 м/мин (0,1167 м/с), высота подъема груза Н=14 м, режим работы – 8М.
  Требуется:
  1) определить мощность электродвигателя и подобрать его по каталогу;
  2) определить общее передаточное число механизма подъема, выбрать тип передач, сделать кинематический расчет;
  3) выбрать тип тормоза произвести его расчет и подобрать по каталогу электромагнит;
  4) рассчитать канат и подобрать его по ГОСТ-ИСО;
  5) определить диаметр, длину, канатоемкость и толщину стенок барабана и проверить барабан на прочность;
  6) определить диаметры блоков;
  7) выбрать по ГОСТу крюк.

  2. Рассчитать ленточный конвейер
  Расчетная часовая производительность конвейера Q=170 т/ч
  Насыпная плотность транспортируемого материала ρ=0,9т/м³
  Длины участков по горизонтали l1=16м; l2=35м
  Угол наклона конвейера β=12
  Скорость транспортируемого материала v=1,4 м/с.
  Требуется:
  1) определить ширину ленты с округлением ее до ближайшей стандартной;
  2) вычислить силы сопротивления движению ленты на всех участках конвейера;
  3) определить силы натяжения ленты и тяговое усилие на приводном барабане;
  4) по максимальному натяжению ленты определить число прокладок и толщину ее;
  5) выбрать конструкцию поддерживающих роликов и барабанов и определить их диаметры;
  6) определить мощность электродвигателя и подобрать его по каталогу;
  7) определить общее передаточное число привода конвейера, наметить тип передач и определить передаточное число каждой передачи

  Методичка здесь
  метод задачи к контрольным заданиям Меновщиков В.А

  1.00 $ В корзину
• 

  Детали машин задачи группа 9 вариант 3

  Описание

  1. Рассчитать механизм подъема мачтовострелового крана
  Вес груза F=22 кН, скорость подъема груза v=11 м/мин, высота подъема груза Н=16 м, режим работы – 2М.
  Требуется:
  1) определить мощность электродвигателя и подобрать его по каталогу;
  2) определить общее передаточное число механизма подъема, выбрать тип передач, сделать кинематический расчет;
  3) выбрать тип тормоза произвести его расчет и подобрать по каталогу электромагнит;
  4) рассчитать канат и подобрать его по ГОСТ-ИСО;
  5) определить диаметр, длину, канатоемкость и толщину стенок барабана и проверить барабан на прочность;
  6) определить диаметры блоков;
  7) выбрать по ГОСТу крюк.

  2. Рассчитать пластинчатый конвейер
  Требуется:
  1) определить ширину ленты с округлением ее до ближайшей стандартной;
  2) вычислить силы сопротивления движению несущего полотна на всех участках конвейера;
  3) определить силы натяжения тяговой цепи и тяговое уси¬лие на приводной звездочке;
  4) по максимальному натяжению выбрать тяговый орган конвейера;
  5) выбрать конструкции направляющих роликов и приводную звездочку, определить их диаметры;
  6) определить мощность электродвигателя;
  7) определить общее передаточное число привода конвейера; наметить тип пере¬дач и определить передаточное число каждой передачи.
  Исходные данные:
  Q=180 – расчетная часовая производительность конвейера, т/ч;
  Плотность транспортируемого материала ρ=2,1т/м³
  Длины участков по горизонтали l1 = 35 м, l2 = 85 м,
  Угол наклона конвейера β=18
  Скорость транспортируемого материала v=0,7 м/с.

  Методичка здесь
  метод задачи к контрольным заданиям Меновщиков В.А

  1.00 $ В корзину
• 

  Деталі машин курсова Мелітополь

  Описание

  1. Тяговий та силовий розрахунок стрічкового транспортера
  2. Розрахунок геометричних розмірів барабана стрічкового транспортера

  18 сторіннок

  3.00 $ В корзину
• 

  Джерела конституційного права: поняття та види

  Описание

  Зміст
  Джерела конституційного права: поняття та види
  Культурні права людини і громадянина в Україні
  Конституційний статус Президента України
  Список літератури

  Методичка тут
  метод Конституційне право П

  1.00 $ В корзину
• 

  Джерела права Європейського Союзу, реферат

  Описание

  Зміст

  Вступ
  Поняття та види джерел права ЄС
  Первинне право та його джерела
  Джерела вторинного права ЄС
  Висновок
  Список використаних джерел

  Методичка тут
  Методичка Право Європейського Союзу

  1.00 $ В корзину
• 

  Джерела та принципи права соціального забезпечення, реферат март 2019г

  Описание

  Зміст

  Вступ
  Поняття і види джерел права соціального забезпечення. Класифікація джерел права соціального забезпечення
  Конституція України – основне джерело права соціального забезпечення
  Акти міжнародно-правового регулювання соціального забезпечення
  Закони України – провідні джерела права соціального забезпечення
  Підзаконні акти в системі джерел права соціального забезпечення
  Значення актів Конституційного Суду України та судової практики в правовому регулювання відносин у сфері соціального забезпечення
  Акти соціального партнерства джерела права соціального забезпечення
  Поняття та види принципів права соціального забезпечення
  Загальна характеристика принципів права соціального забезпечення
  Всезагальність права на соціальне забезпечення
  Залежність права на соціальне забезпечення від соціального ризику
  Соціальне страхування
  Гарантування соціальним забезпеченням гідного рівня життя особи
  Відповідність соціального забезпечення міжнародним стандартам
  Висновки
  Список використаної літератури

  Відповідно до Конституції України, чинні міжнародні договори, згода на обов’язковість яких надана Верховною Радою України, є частиною національного законодавства України. Якщо міжнародним договором України передбачені інші правила, ніж у законі, то застосовуються правила міжнародного договору [1, ст.9].
  Серед міжнародних документів особливе місце посідає Загальна декларація прав людини, яка передбачила право людини на соціальне забезпечення за допомогою національних зусиль та міжнародного співробітництва й відповідно до структури і ресурсів кожної держави.

  Методичка тут
  Метод ПСЗ 2019

  5.00 $ В корзину
• 

  Дискретная математика вар 10

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 11

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
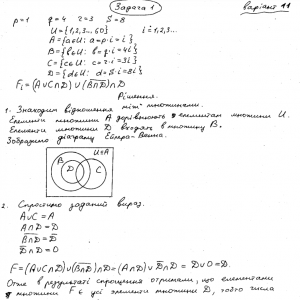
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 12

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 13

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 15

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 17

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 18

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 19

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 2

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 21

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 23

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 24

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 3

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
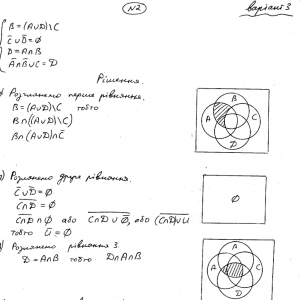
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 4

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички, а также задачи 6 и 8
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  Завдання №6
  Транспортна мережа задана за допомогою таблиці, де зазначені дуги мережі та пропускну спроможність цих дуг. Необхідно зобразити граф графічно і, використовуючи теорему Форда-Фалкерсона, визначити найбільший потік у мережі (s – джерело, t – стік).

  Завдання № 8
  1. Функцію f(x1, x2, x3,x4) записати у вигляді таблиці істинності та у вигляді нормальної та досконалої формах зображення.
  2. Методом резолюцій довести, що одна з формул є логічним наслідком деяких висловів або впевнитись у противному.

  2.50 $ В корзину
• 

  Дискретная математика вар 5

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
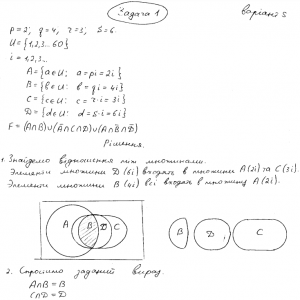
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 6

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 8

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину
• 

  Дискретная математика вар 9

  Описание

  Задачи по дискретной математике и комбинаторике.
  Решены первые 4 задачи из методички
  метод дискретная

  Завдання №1
  Задано універсальну множину U={1,2,3,…,60} та чотири її підмножини А={a∈U: a=p*i}, B={b∈U: b=q*i}, C={c∈U: c=r*i}, D={d∈U: d=s*i}, i=1,2,… Значення p, q,r,s наведено у таблиці.

  Завдання №2
  Задано множини A, B, C, D , що знаходяться в загальному положенні. Необхідно за допомогою діаграм Ейлера-Венна знайти розв’язок системи рівнянь.

  Завдання №3
  Задано граф G. Зобразити граф у вигляді матриць суміжності й суміжності ваг. Знайти найкоротший шлях і його довжину між двома зазначеними вершинами графа (варіант із номером, який кратний 2, – методом Дейкстри, інші варіанти – методом Форда, за необхідності розставивши напрямок дуг від вершини з меншим індексом до вершини з більшим індексом).

  Завдання №4
  Орієнтований граф G=(X,U) задано матрицею суміжності ваг С.
  Необхідно :
  – зобразити граф графічно й у вигляді матриці інциденцій;
  – визначити хроматичне число графа;
  – використовуючи метод Шимбела, визначити найкоротші відстані між будь-якими двома вершинами графа.

  2.00 $ В корзину